Układ równań i nierówności drugiego stopnia
Jeżeli jedno z równań lub nierówności układu równań (układu nierówności) jest drugiego stopnia, a stopień drugiego równania lub nierówności nie jest większy od 2, to układ taki nazywamy układem drugiego stopnia.
Przykłady
Oto kilka przykładów układów równań (nierówności) drugiego stopnia:
\(\begin{cases}5x^2-4y^2+xy+5x-5y+6=0\\x-y=1\end{cases}\)
\({\begin{cases}5x^2-4y^2\geq{0}\\2x-y^2=1\end{cases}}\)
\({\begin{cases}xy+x-y\leq{0}\\x^2-y^2\geq{-1}\end{cases}}\)
Najczęściej układy tego typu rozwiązujemy metodą podstawiania.
Rozwiązać taki układ, to znaczy znaleźć wszystkie pary liczb, które są jednocześnie rozwiązaniem jednego, jak i drugiego równania (nierówności) lub wykazać, że układ nie ma rozwiązań.
Interpretacją geometryczną rozwiązania układu równań (nierówności) są punkty wspólne (ich współrzędne spełniają układ) wykresów każdego z równań (nierówności) tego układu.
Przykład 1
Rozwiążemy dla przykładu układ równań:
\(\begin{cases}x^2+y^2=8\\x=y\end{cases}\)
\({\begin{cases}x^2+x^2=8\\x=y\end{cases}}\)
\({\begin{cases}2x^2=8\\x=y\end{cases}}\)
\({\begin{cases}x^2=4\\x=y\end{cases}}\)
\({\begin{cases}x=2\\x-y=1\end{cases}\vee\begin{cases}x=-2\\x-y=1\end{cases}}\)
\({\begin{cases}x=2\\y=2\end{cases}\vee\begin{cases}x=-2\\y=-2\end{cases}}\)
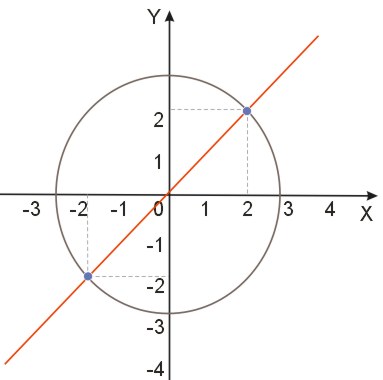
Zatem układ ma dwa rozwiązania. Są to pary liczb \((2,2)\) oraz \((-2,-2)\). Wykresy obu równań powinny się przecinać właśnie w tych punktach. Pierwsze równanie jest równaniem okręgu o środku \(S(0,0)\) i promieniu\(r=\sqrt{8}=2\sqrt{2}\), wykresem drugiego równania jest prosta.
Przykład 2
Rozwiążemy teraz graficznie układ:
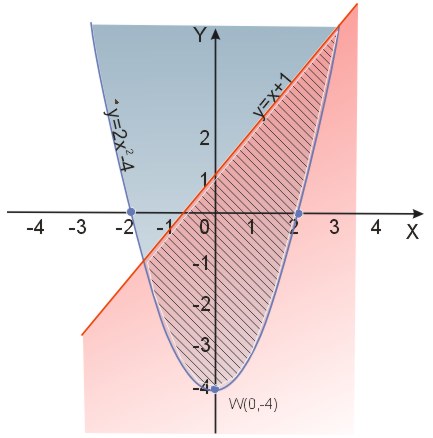
\(\begin{cases}y\geq{2x^2-4}\\y\leq{x+1}\end{cases}\)
Na niebiesko zaznaczono wykres pierwszej nierówności, na czerwono — drugiej. Zakreskowana figura, to graficzne rozwiązanie układu.
Zadania z rozwiązaniami

Zadanie nr 1.
Rozwiązać graficznie i rachunkowo układ równań
\(\begin{cases} (x-2)^2+(y-2)^2=1 \\ y=x+1 \end{cases}\)

Zadanie nr 2.
Rozwiązać graficznie i rachunkowo układ równań
\(\begin{cases} xy-2=0 \\ y=-3x+3 \end{cases}\)

Zadanie nr 3.
Rozwiązać graficznie i rachunkowo układ równań
\(\begin{cases} x^2+y^2=4 \\ xy=1 \end{cases}\)

Zadanie nr 4.
Rozwiązać graficznie i rachunkowo układ równań:
a) \(\begin{cases} (x+1)^2+(y+1)^2=4 \\ x=3 \\y=1 \end{cases}\)
b) \(\begin{cases} (x-1)^2+(y-1)^2=4 \\ x=3 \\y=1 \end{cases}\)

Zadanie nr 5.
Rozwiązać graficznie układ równań:
\(\begin{cases} (x-1)^2+(y-1)^2=2 \\ y=x^2 \end{cases}\)

Zadanie nr 6.
Dla jakich wartości parametru m układ równań:
\(\begin{cases} x^2+y^2=4 \\ y=3x+m \end{cases}\)
a) nie posiada rozwiązań
b) posiada jedno rozwiązanie
c) posiada dwa rozwiązania
d) posiada nieskończenie wiele rozwiązań?

Zadanie nr 7.
Rozwiązać graficznie i rachunkowo układ równań:
\(\begin{cases} y=\frac{1}{4}x^2-x+1 \\ (x-2)^2+(y-2)^2=4 \end{cases}\)

Zadanie nr 8.
Rozwiązać graficznie układy nierówności:
a) \(\begin{cases} (x-2)^2+(y-2)^2\leq 4 \\ (x-2)^2+(y-2)^2\geq 1 \end{cases}\)
b) \(\begin{cases} (x-1)^2+y^2\leq 4 \\ (x+1)^2+y^2\leq 4 \end{cases}\)

Zadanie nr 9.
Rozwiązać graficznie układ nierówności:
\(\begin{cases} x^2+y^2\leq 4 \\ y<x \\y>-x \end{cases}\)

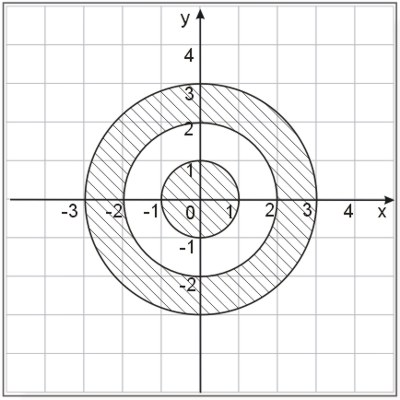
Zadanie nr 10.
Zapisz za pomocą wzoru zbiór przedstawiony na rysunku (zakreskowane pole).

Zadanie nr 11 — maturalne.
W kartezjańskim układzie współrzędnych \((x,y)\) prosta \(l\) o równaniu \(x-y-2=0\) przecina parabolę o równaniu \(y=4x^2-7x+1\) w punktach \(A\) oraz \(B\). Odcinek \(AB\) jest średnicą okręgu \(O\). Punkt \(C\) leży na okręgu \(O\) nad prostą \(l\), a kąt \(BAC\) jest ostry i ma miarę \(\alpha\) taką, że \(tg\alpha=\frac{1}{3}\) (zobacz rysunek).
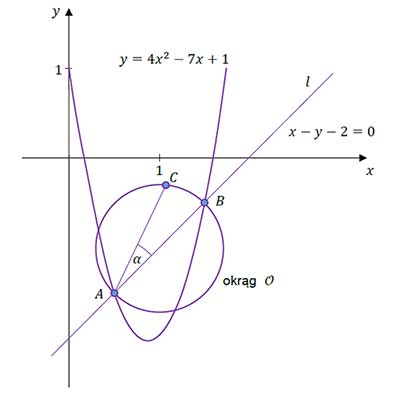
Oblicz współrzędne punktu \(C\). Zapisz obliczenia.
© medianauka.pl, 2009-08-16, A-278
Data aktualizacji artykułu: 2023-05-08
