Układ równań
Jeżeli mamy dwa równania, to może się zdarzyć, że pewna para liczb spełnia zarówno jedno, jak i drugie równanie (spełnia jednocześnie oba równania). Powyższe możemy zapisać, używając do tego celu klamry, która zastępuje słowo "i". Takie równania spięte klamrą będziemy nazywać układem równań.
\(\begin{cases}a_1x+b_1y=c_1\\a_2x+b_2y=c_2\end{cases}\)
Jeżeli oba równania w układzie równań są równaniami pierwszego stopnia, to układ taki nazywamy układem dwóch równań pierwszego stopnia z dwiema niewiadomymi.
Rozwiązanie układu równań
Każdą parę liczb \((x,y)\), która jest jednocześnie rozwiązaniem dwóch równań, nazywamy rozwiązaniem układu tych równań.
Przykłady
Oto przykład układu równań:
\(\begin{cases}2x+y=0\\x-y=1\end{cases}\)
Para liczb \((\frac{1}{3},-\frac{2}{3})\) jest rozwiązaniem powyższego układu równań. Możemy to sprawdzić, podstawiając te liczby do obu równań.
\(\begin{cases}2\cdot \frac{1}{3}+(-\frac{2}{3})=0 \\ \frac{1}{3}-(-\frac{2}{3})=1 \end{cases}\)
\(\begin{cases} 0=0 \\ 1=1 \end{cases}\)
Rozwiązać układ równań to znaczy znaleźć wszystkie rozwiązania tego układu równań albo wykazać, że jest nim zbiór pusty. Zbiór rozwiązań układu równań jest iloczynem rozwiązań (częścią wspólną) wszystkich zbiorów rozwiązań poszczególnych równań układu.
Interpretacja geometryczna układu równań
Wykresami równań pierwszego stopnia z dwiema niewiadomymi są proste. Proste mogą się przecinać w jednym punkcie, być równoległe lub pokrywać się.
1) Jeżeli proste przecinają się w jednym punkcie, to układ równań nazywamy układem równań niezależnych.
Para liczb, będąca współrzędnymi punktu przecięcia się obu prostych stanowi rozwiązanie tego układu.
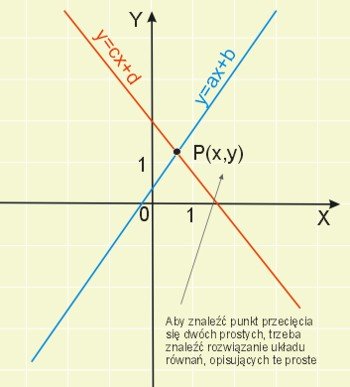
2) Jeżeli proste są równoległe, to układ równań nazywamy układem równań sprzecznych.
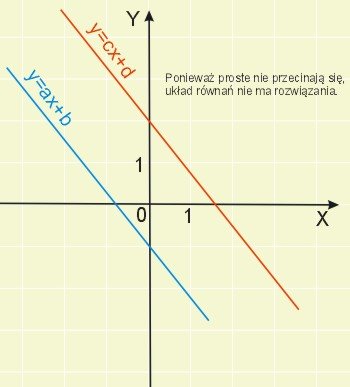
3) Jeżeli proste pokrywają się, to układ równań nazywamy układem równań zależnych.
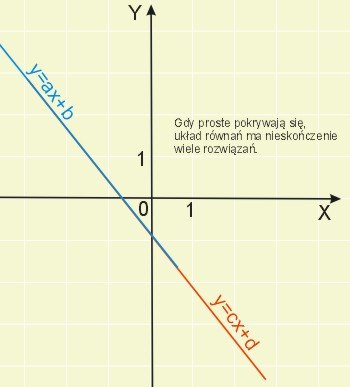
Inne układy równań
Czasem rozpatrujemy układy wielu równań z wieloma zmiennymi. Poniżej przykłady takich układów.
Przykłady
\(\begin{cases}2x-3x=0\\-x-y=-4\\55x-22y=-18\end{cases}\)
\(\begin{cases}x+y+z=0\\2x-y-5z=4\\-x-2y-12z=8\end{cases}\)
W zależności od tego, co jest wykresem poszczególnych równań, zawsze układ tych równań reprezentuje część wspólna wykresów poszczególnych równań.
Rozwiązywanie układu równań
Metoda podstawiania
Jedną z metod rozwiązywania układów równań jest metoda podstawiania, która polega na wyznaczeniu w jednym z równań układu jednej niewiadomej poprzez drugą niewiadomą i wstawieniu tak otrzymanego wyrażenia do drugiego równania. Układ złożony z wyznaczonego równania i przekształconego drugiego równania będzie układem równoważnym do danego. Układ równoważny otrzymamy także wówczas, jeżeli dowolne równanie układu zastąpimy równaniem równoważnym.
A oto przykłady na układy równań sprzecznych i zależnych:
Przykład
Rozwiąż układ równań metodą podstawiania.
\(\begin{cases}x-y=0\\y-x=1\end{cases}\)
\(\begin{cases}x=y\\y-y=1\end{cases}\)
\(\begin{cases}x=y\\0=1\end{cases}\)
Rozpatrywany układ jest układem równań sprzecznych.
Przykład
Rozwiązać układ równań metodą podstawiania.
\(\begin{cases}x-y=0\\2x-2y=0\end{cases}\)
\(\begin{cases}x=y\\2y-2y=0\end{cases}\)
\(\begin{cases}x=y\\0=0\end{cases}\)
Rozpatrywany układ jest układem równań zależnych.
Metodą podstawiania możemy rozwiązywać także układy trzech, czterech i większej liczby równań. Warto jednak zwrócić uwagę na to, aby podczas wybierania równań do wyznaczania zmiennych wybierać możliwie najprostsze równania w celu ułatwienia rachunków. Metoda ta jest metodą najczęściej wykorzystywaną przez uczniów w szkołach ze względu na swoją prostotę. Niestety bywa nieefektywna. Warto zapoznać się z metodą przeciwnych współczynników, często stosowaną razem z metodą podstawiania oraz z metodą wyznaczników, która w skomplikowanych układach, w szczególności z parametrem daje najszybsze efekty.
Metoda przeciwnych współczynników
Jedną z metod rozwiązywania układów równań jest metoda przeciwnych współczynników, która polega na takim pomnożeniu obu stron jednego lub obu równań przez liczbę różną od zera, żeby otrzymać liczby przeciwne przy jednej z niewiadomych i dodaniu do siebie obu równań. Układ złożony z jednego równania i sumy obu równań jest układem równoważnym do danego.
Poniższa animacja ilustruje opisywaną wyżej metodę rozwiązywania układu równań.
Przykład
Rozwiąż układ równań metodą przeciwnych współczynników.
\(\begin{cases} x-y=0\\y-x=1 \end{cases}\)
\(\begin{cases}x-y=0\\\underline{-x+y=1}\end{cases}\)
\(\quad 0=1\)
Rozpatrywany układ jest układem równań sprzecznych.
Przykład
Rozwiązać układ równań metodą przeciwnych współczynników.
\(\begin{cases}x-y=0/\cdot(-2)\\2x-2y=0\end{cases}\)
\(\begin{cases}-2x+2y=0\\ \underline{2y-2y=0}\end{cases}\)
\(\quad 0=0\)
Rozpatrywany układ jest układem równań zależnych.
Pytania
Czy są inne metody rozwiązywania układów równań?
Tak. To rozwiązywanie układów równań metodą wyznaczników.
Kiedy układ równań ma nieskończenie wiele rozwiązań?
Układ równań ma nieskończenie wiele rozwiązań, gdy jest to układ równań zależnych. Jak to stwierdzić? Najlepiej użyć metody wyznaczników, która został opisania w odrębnym artykule, do którego link znajdziesz niżej.
Zadania z rozwiązaniami

Zadanie nr 1.
Znaleźć współrzędne punktu przecięcia się prostych o równaniach \(y=3x-5\) oraz \(y=-5x+3\)

Zadanie nr 2.
Rozwiązać układ równań metodą podstawiania:
a) \(\begin{cases} 3x-2y=-4 \\ x+3y=-5\end{cases}\)
b) \(\begin{cases} \sqrt{3}x+4y=1\\ x+2\sqrt{3}y=\sqrt{3}\end{cases}\)

Zadanie nr 3.
Rozwiązać układ równań metodą podstawiania:
a) \(\begin{cases} y-3x=2\\ -2y+6x=1 \end{cases}\)
b) \(\begin{cases} 2x+\frac{1}{2}y=\frac{1}{3}\\ -12x-3y=-2 \end{cases}\)

Zadanie nr 4.
Rozwiązać układ równań metodą przeciwnych współczynników:
a) \(\begin{cases} \frac{1}{2}x-2=y\\ \frac{1}{3}x+3=\frac{1}{4}y \end{cases}\)
b) \(\begin{cases} 5x+5y=-7\\ -3x-2y=4 \end{cases}\)

Zadanie nr 5.
Rozwiązać układ równań metodą przeciwnych współczynników:
a) \(\begin{cases} \sqrt{2}x-\sqrt{6}y=\sqrt{5}\\ 2x+4y=\sqrt{10} \end{cases}\)
b) \(\begin{cases} 2x+y=-\frac{1}{2}\\ -4x-2y=1 \end{cases}\)
c) \(\begin{cases} 3x-y=5\\-6x+2y=-1 \end{cases}\)

Zadanie nr 6 — maturalne.
Proste o równaniach \(2x-3y=4\) i \(5x-6y=7\) przecinają się w punkcie \(P\). Stąd wynika, że:
A. \(P=(1,2)\)
B. \(P=(-1,2)\)
C. \(P=(-1,-2)\)
D. \(P=(1,-2)\)

Zadanie nr 7 — maturalne.
Proste o równaniach \(2x-3y=4\) i \(5x-6y=7\) przecinają się w punkcie \(P\). Stąd wynika, że:
A. \(P=(1,2)\)
B. \(P=(-1,2)\)
C. \(P=(-1,-2)\)
D. \(P=(1,-2)\)

Zadanie nr 8 — maturalne.
Wyznacz wszystkie wartości parametru \(a\), dla których wykresy funkcji \(f\) i \(g\), określonych wzorami \(f(x)=x-2\) oraz \(g(x)=5-ax\), przecinają się w punkcie o obu współrzędnych dodatnich.

Zadanie nr 9 — maturalne.
Układ równań
\(\begin{cases}x-y=3\\ 2x+0,5y=4 \end{cases}\)
opisuje w układzie współrzędnych na płaszczyźnie:
A. zbiór pusty.
B. dokładnie jeden punkt.
C. dokładnie dwa różne punkty.
D. zbiór nieskończony.

Zadanie nr 10 — maturalne.
W układzie współrzędnych są dane punkty \(A=(-43,-12)\), \(B=(50,19)\). Prosta AB przecina oś \(Ox\) w punkcie \(P\). Oblicz pierwszą współrzędną punktu \(P\).

Zadanie nr 11 — maturalne.
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
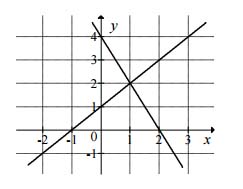
Wskaż ten układ:
A. \(\begin{cases}y=x+1\\y=-2x+4\end{cases}\)
B. \(\begin{cases}y=x-1\\y=2x+4\end{cases}"\)
C. \(\begin{cases}y=x-1\\y=-2x+4\end{cases}"\)
D. \(\begin{cases}y=x+1\\y=2x+4\end{cases}\)

Zadanie nr 12 — maturalne.
Para liczb \(x=2\) i \(y=2\) jest rozwiązaniem układu równań
\(\begin{cases} ax+y=5\\-2x+3y=2a\end{cases}\)
dla:
A. \(a=-1\)
B. \(a=1\)
C. \(a=-2\)
D. \(a=2\)

Zadanie nr 13 — maturalne.
Na rysunku obok przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań. Wskaż ten układ, którego geometryczną interpretację przedstawiono na rysunku.
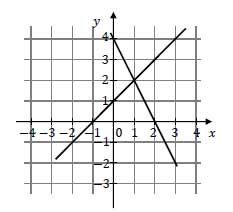
A. \(\begin{cases}y=x+1\\y=-2x+4\end{cases}\)
B. \(\begin{cases}y=x-1\\y=2x+4\end{cases}\)
C. \(\begin{cases}y=x-1\\y=2x+4\end{cases}\)
D. \(\begin{cases}y=x+1\\y=2x+4\end{cases}\)

Zadanie nr 14 — maturalne.
Prosta przechodząca przez punkty \(A=(8, −6)\) i \(B=(5, 15)\) jest styczna do okręgu o środku w punkcie \(O=(0, 0)\). Oblicz promień tego okręgu i współrzędne punktu styczności tego okręgu z prostą AB.

Zadanie nr 15 — maturalne.
Rozwiązaniem układu równań \(\begin{cases} 11x-11y=1\\22x+22y=-1\end{cases}\) jest para liczb \(x=x_0, y=y_0\). Wtedy
A. \(x_0>0\) i \(y_0>0\)
B. \(x_0>0\) i \(y_0<0\)
C. \(x_0<0\) i \(y_0>0\)
D. \(x_0<0\) i \(y_0<0\)

Zadanie nr 16.
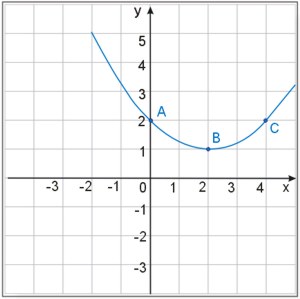
Znaleźć równanie paraboli, której fragment przedstawiono na rysunku:
Powiązane materiały
Ćwiczenia, sprawdziany i quizy
 Układy równań
Układy równań© medianauka.pl, 2009-07-03, A-260
Data aktualizacji artykułu: 2023-05-03

 Rozwiązywanie układów równań — metoda wyznaczników
Rozwiązywanie układów równań — metoda wyznaczników Układ równań pierwszego stopnia
Układ równań pierwszego stopnia



