Metoda wyznaczników
Jedną z metod rozwiązywania układów równań jest metoda wyznaczników. Metoda ta należy do najefektywniejszych metod rozwiązywania układów równań, szczególnie tych z parametrem. Zanim jednak zostanie omówiona ta metoda, należy zapoznać się z pojęciem wyznacznika.
Definicja
Różnicę iloczynów \(ad-bc\) nazywamy wyznacznikiem drugiego stopnia i oznaczamy go w następujący sposób: \(W=\left|\begin{array}{cc}a&b\\c&d\end{array}\right|\)
Liczby w wyznaczniku mnożymy „na krzyż”.
Przykłady
\(W=\left|\begin{array}{cc}1&2\\3&4\end{array}\right|=1\cdot{4}-2\cdot{3}=4-6=-2\)
\(W=\left|\begin{array}{cc}5&-2\\4&3\end{array}\right|=5\cdot{3}-(-2\cdot{4})=15+8=23\)
\(W=\left|\begin{array}{cc}0&4\\0&3\end{array}\right|=0\cdot{3}-4\cdot{0}=0-0=0\)
Wyznacznik układu
Dany jest układ równań:
\(\begin{cases}a_1x+b_1y=c_1\\a_2x+b_2y=c_2\end{cases}\)
Wyznacznik układu jest to:
\(W=\left|\begin{array}{cc}a_1&b_1\\a_2&b_2\end{array}\right|\)
Zapisujemy więc w wyznaczniku kolejno wszystkie liczby przy niewiadomych w odpowiedniej kolejności.
Wyznacznik ze względu na \(x\) jest to:
\(W_x=\left|\begin{array}{cc}c_1&b_1\\c_2&b_2\end{array}\right|\)
Zastępujemy więc w wyznaczniku układu liczby stojące przy niewiadomej \(x\) wyrazami wolnymi \(c\).
Wyznacznik ze względu na \(y\) jest to:
\(W_y=\left|\begin{array}{cc}a_1&c_1\\a_2&c_2\end{array}\right|\)
Zastępujemy więc w wyznaczniku układu liczby stojące przy niewiadomej \(y\) wyrazami wolnymi \(c\).
Znając wyznaczniki układu, możemy łatwo określić jego rozwiązanie. Możliwe są trzy przypadki:
1) Jeżeli \(W\neq{0}\), to układ równań ma dokładnie jedno rozwiązanie:
2) Jeżeli \(W=W_x=W_y=0\), to układ równań ma nieskończenie wiele rozwiązań, równania układu są od siebie zależne.
3) Jeżeli \(W=0\quad{i}\quad{W_x}\neq{0}\) lub \(W=0\quad{i}\quad{W_y}\neq{0}\) to układ równań nie ma rozwiązań, jest to układ równań wzajemnie sprzecznych.
Przykłady
Rozwiązać układ równań metodą wyznaczników:
\(\begin{cases}5x+4y-1=0\\-y-3=-x\end{cases}\)
W pierwszej kolejności należy uporządkować wyrazy. Wyrazy wolne przenosimy na prawą stronę równań, niewiadome w odpowiedniej kolejności na lewą stronę równań.
\(\begin{cases}5x+4y=1\\x-y=3\end{cases}\)
Obliczamy wyznacznik układu:
\(W=\left|\begin{array}{cc}5&4\\1&-1\end{array}\right|=5\cdot(-1)-4\cdot{1}=-5-4=-9\)
Wyznacznik układu jest różny od zera, więc układ posiada jedno rozwiązanie. Aby je znaleźć, musimy obliczyć wyznacznik ze względu na \(x\), zastępując współczynniki przy tej niewiadomej wyrazami wolnymi:
\(W_x=\left|\begin{array}{cc}1&4\\3&-1\end{array}\right|=1\cdot(-1)-4\cdot{3}=-1-12=-13\)
oraz obliczamy wyznacznik ze względu na \(y\), zastępując w wyznaczniku współczynniki stojące przy \(y\) wyrazami wolnymi:
\(W=\left|\begin{array}{cc}5&1\\1&3\end{array}\right|=5\cdot{3}-1\cdot{1}=15-1=14\)
Mamy więc rozwiązanie:
\(x=\frac{W_x}{W}=\frac{-13}{-9}=1\frac{4}{9}\)
\(y=\frac{W_y}{W}=\frac{14}{-9}=-1\frac{5}{9}\)
Kalkulator układów równań

Rozwiązywanie układów równań metodą wyznacznikową
Nasz robot spróbuje rozwiązać układ równań liniowych za pomocą wyznaczników.
Układ dwóch równań pierwszego stopnia ma postać:
\(\begin{cases} a_1x+b_1y=c_1 \\ a_2x+b_2y=c_2\end{cases}\)
Jeżeli twój układ nie ma takiej postaci, w pierwszej kolejności doprowadź go do niej, porządkując wyrazy przy niewiadomych i wyrazy wolne. Aby rozwiązać układ równań, podaj współczynniki \(a_1, b_1, c_1, a_2, b_2, c_2\):
Wpisz dane:x+ y =
Układy równań z parametrem
Metoda wyznaczników sprawdza się wyjątkowo dobrze w przypadku układów równań z parametrem. Oto przykład takiego zadania.
Przykłady
Dla jakiej wartości parametru \(m\), układ równań
\(\begin{cases}(m-1)x+4y=0\\x-2y=m+2\end{cases}\)
ma jedno rozwiązanie?
Obliczamy wyznacznik układu:
\(W=\left|\begin{array}{cc}m-1&4\\1&-2\end{array}\right|=(m-1)\cdot(-2)-4\cdot{1}=-2m+2-4=-2m-2\)
Aby układ równań miał jedno rozwiązanie, wyznacznik układu musi być różny od zera, więc
\(-2m-2\neq{0}\)
\(-2m\neq{2}/:(-2)\)
\(m\neq{-1}\)
Dla \(m\) różnego od -1 układ równań ma jedno rozwiązanie.
Znajdźmy to rozwiązanie. Musimy obliczyć wyznacznik ze względu na \(x\), zastępując wyrazami wolnymi współczynniki przy tej niewiadomej:
\(W_x=\left|\begin{array}{cc}0&4\\m+2&-2\end{array}\right|=0-4(m+2)=-4m-8\)
oraz obliczamy wyznacznik ze względu na \(y\), zastępując w wyznaczniku współczynniki stojące przy \(y\) wyrazami wolnymi:
\(W=\left|\begin{array}{cc}m-1&0\\1&m+2\end{array}\right|=(m-1)(m+2)-0\cdot{1}=m^2+m-2\)
Mamy więc rozwiązanie:
\(x=\frac{W_x}{W}=\frac{-4m-8}{-2m-2}=\frac{-2(2m+4)}{-2(m+1)}=\frac{2m+4}{m+1}\)
\(y=\frac{W_y}{W}=\frac{m^2+m-2}{-2m-2}\)
Zadania z rozwiązaniami

Zadanie nr 1.
Dla jakiej wartości parametru \(a\) układ równań
\(\begin{cases} (a+1)x-3y+a=0 \\ ax+y+a+1=0 \end{cases}\)
nie ma rozwiązania?

Zadanie nr 2.
Dla jakiej wartości parametrów \(a, b, c\) układ równań
\(\begin{cases} (a+1)x-y=b \\ 2ax+y=c \end{cases}\)
ma nieskończenie wiele rozwiązań?

Zadanie nr 3.
Dla jakiej wartości parametru \(a\) układ równań
\(\begin{cases} (a-2)x+y=-3a+1 \\ -4x+(a+4)y=a-1 \end{cases}\)
ma jedno rozwiązanie?

Zadanie nr 4.
Rozwiązać układ równań
\(\begin{cases} \sqrt{2}x-(\sqrt{2}-1)y=3-2\sqrt{2} \\ (2+\sqrt{2})x+\sqrt{2}y=-2 \end{cases}\)

Zadanie nr 5.
Rozwiązać układ równań
\(\begin{cases} \frac{x-y}{2}=x+2 \\ y-x=\frac{x+1}{3} \end{cases}\)
Powiązane materiały
© medianauka.pl, 2009-07-12, A-264
Data aktualizacji artykułu: 2023-05-04

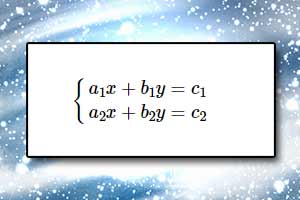 Układ równań
Układ równań Układ równań pierwszego stopnia
Układ równań pierwszego stopnia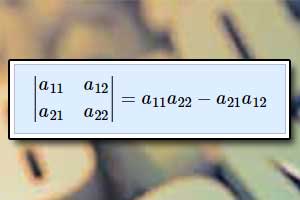 Wyznacznik macierzy
Wyznacznik macierzy