Geometria
Geometria to dział w matematyki, który zajmuje się badaniem figur geometrycznych oraz związków, jakie między nimi zachodzą. To jedna z najstarszych dziedzin matematyki. Zajmowano się nią już w starożytności. Są z nią związani tacy matematycy jak Pitagoras, Euklides, Tales czy Arystoteles. W kursie szkolnym spotykamy się tylko z geometrią euklidesową. Odrzucenie piątego postulatu Euklidesa, który mówi o tym, że na płaszczyźnie przez punkt nieleżący na prostej można przeprowadzić dokładnie jedną prostą równoległą do danej prostej) doprowadziło do powstania nowych geometrii (na przykład Bolyai-Łobaczewskiego, Minkowskiego, która posłużyła do opisu szczególnej teorii względności Einsteina).
Działy
Na skróty
Podstawowe twierdzenia geometrii
Zastosowanie geometrii
Powstanie geometrii wiązało się z poszukiwaniem odpowiedzi na pytania, jakie stawiali sobie budowniczy i handlarze już w starożytności. To dlatego jej początki dotyczą określenia zasad dokonywania pomiarów materialnych rzeczy (na przykład podziału gruntów). Geometria znalazła swoje zastosowanie w architekturze, sztuce, fizyce (optyka geometryczna, grawitacja, szczególna teoria względności), astronomii (trajektorie ruchu ciał niebieskich, mechanika nieba).
Dyscypliny geometrii
Oto wybrane działy geometrii oprócz planimetrii, stereometrii i trygonometrii, które wyszczególniono wyżej.
- Geometria analityczna – dział geometrii zajmujący się badaniem figur geometrycznych metodami analitycznymi (obliczeniowymi) i algebraicznymi. Zagadnienia geometryczne są tu sprowadzane do rozwiązywania układów równań, które opisują badane figury. Za twórcę geometrii analitycznej uważa się Kartezjusza, który w 1837 roku opublikował swoje dzieło Geometria.
- Geometria wykreślna – dział geometrii zajmujący się jednoznacznym odwzorowaniem figur przestrzennych na płaszczyźnie. Proces ten oraz jego efekty nazywa się rzutowaniem. Nauka ta powstała pod koniec XVIII wieku dzięki pracom francuskiego matematyka Gasparda Monge'a.
- Geometria algebraiczna - dział geometrii, który zajmuje się badaniem zbiorów opisywanych za pomocą funkcji wielomianowych.
- Geometria euklidesowa - najstarszy dział geometrii, badający tak zwaną trójwymiarową przestrzeń Euklidesa. To taka geometria, w której są spełnione wszystkie aksjomaty Euklidesa. Geometria ta jest zdefiniowana za pomocą aksjomatów, które określają takie pojęcia jak przestrzeń, punkt, prosta, płaszczyzna, relacja położenia punktu między innymi dwoma punktami oraz relacja przystawania pary punktów do innej pary punktów.
- Geometria absolutna - geometria oparta wyłącznie na czterech pierwszych aksjomatach Euklidesa. Twierdzenia geometrii absolutnej są prawdziwe w geometrii euklidesowej i nieeuklidesowych.
- Geometrie nieeuklidesowe - są to geometrie, odrzucające piąty aksjomat Euklidesa, który mówi o tym, że przez każdy punkt przechodzi co najwyżej jedna prosta równoległa do danej prostej. Geometria nieeuklidesowa mimo, że wydaje się zupełnie abstrakcyjna, znalazła zastosowanie praktyczne w fizyce (szczególna teoria względności Einsteina). Do takich geometrii zalicza się następujące działy:
- Geometria Bolyai-Łobaczewskiego, geometria hiperboliczna, która została zbudowana w oparciu o pierwsze cztery aksjomaty Euklidesa i zaprzeczenie piątego aksjomatu Euklidesa (przez każdy punkt nieleżący na danej prostej można przeprowadzić nieskończenie wiele prostych, które nie przecinają tej prostej.
- Geometria Minkowskiego - geometria przestrzeni czterowymiarowej.
- Geometria rzutowa.
- Geometria eliptyczna.
- Geometria na sferze.

Pytania
Kto jest ojcem geometrii?
Za ojca geometrii uważa się Euklidesa - matematyka greckiego z czasów starożytnych. Dlaczego? To on pierwszy zebrał wszystkie myśli ówczesnego świata w dzieło o tytule Elementy. Było to pierwsze podejście aksjomatyczne do zagadnień, którymi zajmuje się geometria. Był to kanon, który obowiązywał aż do XIX wieku! A powstał w III w. p.n.e.
© medianauka.pl, 2016-07-06, A-3199
Data aktualizacji artykułu: 2023-02-05

 Planimetria
Planimetria Stereometria
Stereometria Trygonometria
Trygonometria Rachunek wektorowy
Rachunek wektorowy Przekształcenia geometryczne
Przekształcenia geometryczne Kąty
Kąty Okręgi i koła, elipsy, łuki
Okręgi i koła, elipsy, łuki Trójkąty
Trójkąty Czworokąty
Czworokąty Wielokąt foremny
Wielokąt foremny Twierdzenie Talesa
Twierdzenie Talesa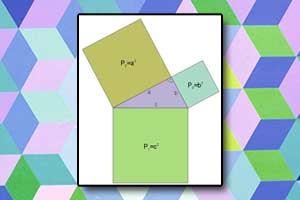 Twierdzenie Pitagorasa
Twierdzenie Pitagorasa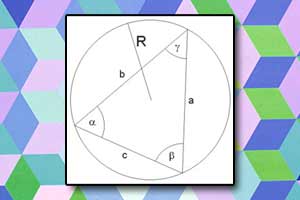 Twierdzenie sinusów, cosinusów, tangensów
Twierdzenie sinusów, cosinusów, tangensów Dlaczego garnki są okrągłe?
Dlaczego garnki są okrągłe? Ile zaoszczędzimy drogi, jadąc po wewnętrznej na zakrętach?
Ile zaoszczędzimy drogi, jadąc po wewnętrznej na zakrętach?