Planimetria
Planimetria to dział geometrii, który bada figury geometryczne i związki między nimi na płaszczyźnie. Planimetria jest geometrią płaszczyzny. Jest budowana na jednej płaszczyźnie, ale stosuje się do każdej innej płaszczyzny. Planimetria bada własności figur geometrycznych płaskich.
Podstawowe pojęcia i twierdzenia planimetrii
TESTY I ZADANIA
Figury geometryczne
W tym miejscu zajmujemy się dowolnymi zbiorami punktów przestrzeni n-wymiarowej, czyli figurami geometrycznymi. Opisujemy podstawowe rodzaje figur geometrycznych, badamy ich własności zarówno na płaszczyźnie jak i w przestrzeni.
Własności figur
Rodzaje figur płaskich
TESTY I ZADANIA
© medianauka.pl, 2023-02-05, A-4685

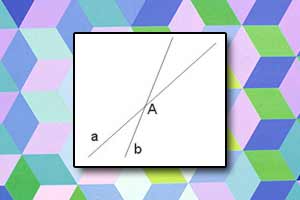 Aksjomaty planimetrii
Aksjomaty planimetrii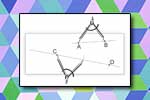 Odległość punktów
Odległość punktów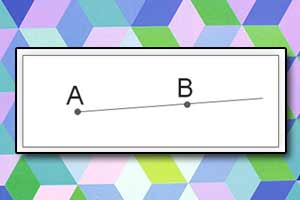 Półprosta
Półprosta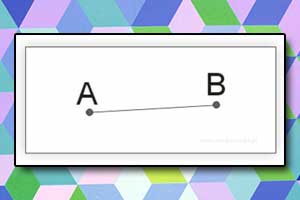 Odcinek
Odcinek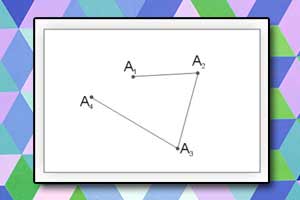 Łamana
Łamana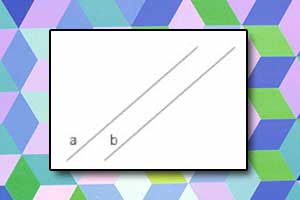 Proste równoległe
Proste równoległe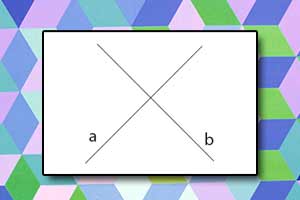 Proste prostopadłe
Proste prostopadłe Pole figury
Pole figury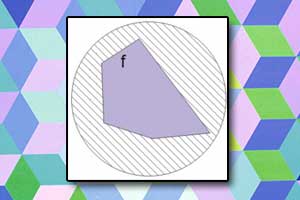 Figura płaska
Figura płaska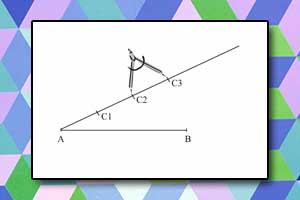 Podział odcinka
Podział odcinka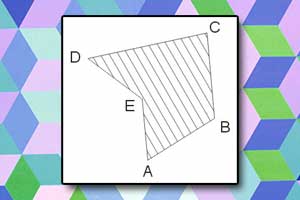 Wielokąt
Wielokąt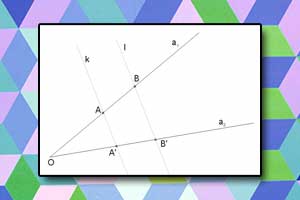 Twierdzenie Talesa
Twierdzenie Talesa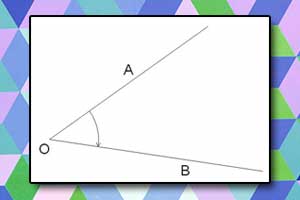 Kąty
Kąty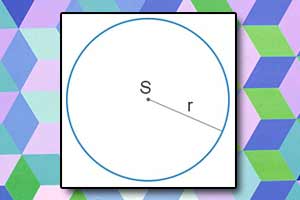 Okręgi i koła, elipsy, łuki
Okręgi i koła, elipsy, łuki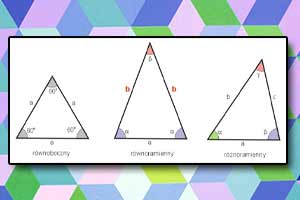 Trójkąty
Trójkąty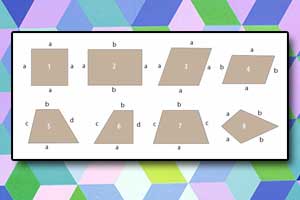 Czworokąty
Czworokąty Wielokąt foremny
Wielokąt foremny