Figura geometryczna

Definicja

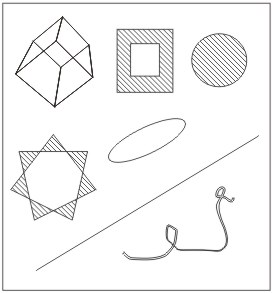
Figura geometryczna jest to dowolny zbiór punktów.

Zbiór wszystkich punktów nazywamy przestrzenią. Każdy możliwy podzbiór przestrzeni to nic innego jak figura geometryczna. Figurą geometryczną jest więc punkt, zbiór złożony z kilku punktów, odcinek, prosta, półprosta, płaszczyzna, bryła i tak dalej.

Figura płaska jest to figura geometryczna, która zawiera się w płaszczyźnie.

Przykład

Oto przykłady figur płaskich: odcinek, prosta, kwadrat, koło, okrąg, trapez.

Figura pusta jest to figura, która nie ma żadnego punktu. Czasem pojęcie to przydaje się przy rozpatrywaniu działań na figurach (zbiorach punktów).

Figura wypukła

Definicja

Jeżeli każdy odcinek o końcach należących do figury f zawiera się w tej figurze, to figurę f nazywamy wypukłą. Figurę, która nie jest wypukła nazywamy niewypukłą.

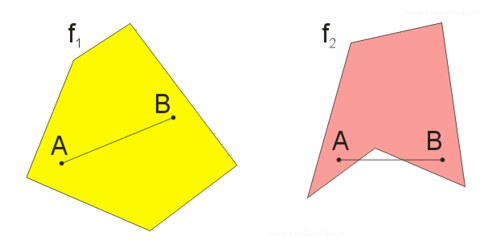
Na powyższym rysunku przedstawiono przykład figury wypukłej (figura f₁) oraz figury niewypukłej (figura f₂), gdzie wyraźnie widać, że część odcinka o końcach należących do figury f₂ leży poza tą figurą.

Przykład

Przykłady figur wypukłych: odcinek, prosta, koło, kwadrat, trapez.

Przykłady figur niewypukłych: łuk, okrąg, zbiór trzech punktów, łamana

Twierdzenie

Iloczyn dwóch figur wypukłych jest figurą wypukłą.

Figura ograniczona

Definicja

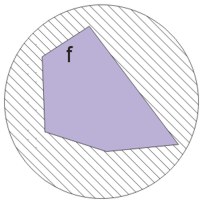
Jeżeli dla danej figury f istnieje koło, w którym się ta figura zawiera, to figurę f nazywamy ograniczoną.

Przykład

Przykłady figur ograniczonych: odcinek, koło, kwadrat, trapez.

Przykłady figur nieograniczonych: prosta, płaszczyzna, półprosta.

Wnętrze, zewnętrze i brzeg figury

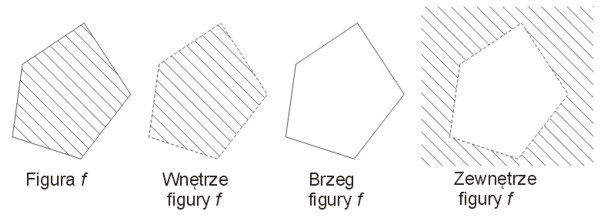
Wnętrze figury jest to zbiór punktów wewnętrznych figury, czyli takich punktów dla których istnieje otoczenie tego punktu, składające się z punktów należących do tej figury.

Zewnętrze figury jest to zbiór punktów zewnętrznych figury, czyli takich punktów dla których istnieje otoczenie tego punktu, składające się z punktów nie należących do tej figury.

Brzeg figury jest to zbiór punktów brzegowych figury, czyli takich punktów, które nie są ani punktami wewnętrznymi ani zewnętrznymi figury.

Aksjomat

Odcinek oraz łuk dowolnego okręgu, który łączy punkt wewnętrzny dowolnej figury z punktem zewnętrznym tej figury, przecina brzeg tej figury co najmniej w jednym punkcie.

Definicja

Figura jest figurą domknięta, jeżeli brzeg figury należy do tej figury.

Definicja

Figura jest figurą otwartą, jeżeli żaden punkt brzegowy tej figury nie należy do tej figury.

Definicja

Figura jest spójna, jeżeli każde dwa punkty tej figury można połączyć łamaną zwyczajną zawartą w tej figurze.

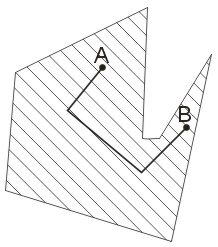
Figura przedstawiona na rysunku znajdującym się po prawej stronie jest przykładem figury spójnej.

Aksjomat

Łamana zwyczajna zamknięta rozcina płaszczyznę na dwie figury spójne, jedną nieograniczoną i drugą - ograniczoną.

Spośród nieskończonej liczby figur geometrycznych na szczególną uwagę zasługują figury, które zostały wymienione poniżej:

Są to podstawowe figury geometryczne, które najczęściej są omawiane w kursach, matematyki. Oprócz wymienionej wyżej przestrzeni, wszystkie wymienione figury to figury geometryczne płaskie. Figury geometryczne przestrzenne (bryły) są tematem osobnego artykułu.

Pytania

Czy odcinek jest wypukły czy wklęsły?

Odcinek jest figurą wypukłą.

Zadania z rozwiązaniami

Zadanie nr 1.

Dane są dowolne proste a i b. Określić figury:
$a\cup b, \ a\cap b, \ a\backslash b, \ b\backslash a$

Pokaż rozwiązanie zadania.

Zadanie nr 2.

Dany jest okrąg k i prosta p przechodząca przez środek okręgu. Opisać figury:
$k\cup p, \ k\cap p, \ k\backslash p, \ p\backslash k$

Pokaż rozwiązanie zadania.

Zadanie nr 3.

Dane są dwa trójkąty t₁ i t₂ usytuowane względem siebie tak, jak pokazuje rysunek.
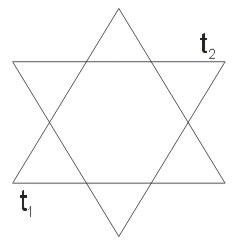
gwiazda

Zakreskować figury:
$a)t_1\cup t_2\\ b)t_1\cap t_2\\ c)t_1\backslash t_2\\ d)t_1\backslash t_2\\ e)(t_1\backslash t_2)\cup (t_2\backslash t_1)$

Pokaż rozwiązanie zadania.

Zadanie nr 4.

Ile maksymalnie prostych może wyznaczyć 10 punktów na płaszczyźnie? A ile w przestrzeni?

Pokaż rozwiązanie zadania.

Zadanie nr 5.

Opisać za pomocą działań na zbiorach część zakreskowaną kół k₁, k₂, k₃
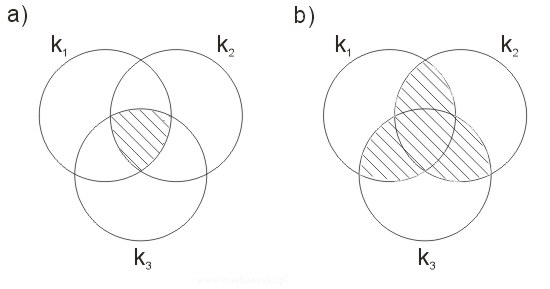
figury

Pokaż rozwiązanie zadania.

Inne zagadnienia z tej lekcji

Podział odcinka

Ilustracja podziału odcinka na równe części. W artykule omówiono także złoty podział odcinka oraz wzory analityczne z tym związane.

Wielokąt

Wielokąt jest to figura geometryczna, która jest sumą łamanej zwyczajnej zamkniętej i części płaszczyzny ograniczonej tą łamaną.

Twierdzenie Talesa

Twierdzenie Talesa - omówienie, przykłady, zadania, twierdzenie odwrotne.

Narysuj 10 figur