Elipsa
Definicja — równanie elipsy
Elipsa jest to linia krzywa określona poprzez następujące równanie:
W równaniu tym \(a>0, \ b>0, \ a\neq b\). Elipsą jest także każda figura otrzymana z tej krzywej przez przekształcenie izometryczne.
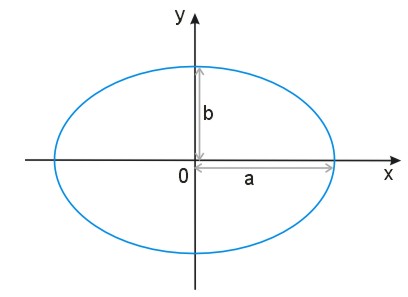
Liczba \(a\) to tak zwana półoś wielka, liczba \(b\), to półoś mała elipsy.
Definicja
Ogniska elipsy są to dwa punkty \(F_1(c,0), F_2(-c,0)\), gdzie liczba \(c\) jest zdefiniowana następująco: \(c^2=a^2-b^2\). Ogniska leżą zawsze na osi wielkiej elipsy i są rozłożone symetrycznie względem środka elipsy.
Ogniskowa elipsy jest to odległość ognisk od siebie. Jest ona równa \(2c\). Liczbę \(c\) nazywamy półogniskową.
Wprowadzone wyżej pojęcia ilustruje poniższy rysunek.
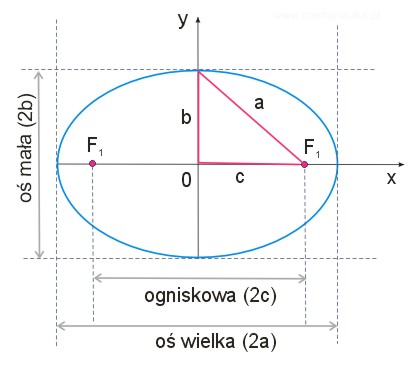
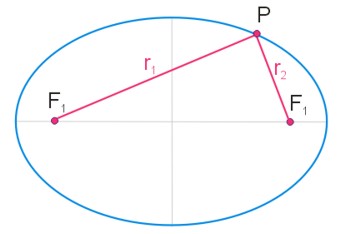
Promienie wodzące punktu elipsy są to odcinki łączące ogniska elipsy z dowolnymi punktami elipsy.
Twierdzenie
Suma promieni wodzących punktu elipsy jest stała i równa długości osi wielkiej elipsy.
\(r_1+r_2=2a=const\)
Powyższa własność pozwala w prosty sposób naszkicować elipsę. Jak narysować elipsę? Ilustruje to krótki film.
 Film
FilmJak narysować elipsę?
Mimośród elipsy
Mimośród elipsy jest to stosunek półogniskowej do półosi wielkiej elipsy. Mimośród oznaczamy zwykle grecką literą \(\varepsilon\).
Ponieważ półogniskowa jest zawsze krótsza od półosi wielkiej w elipsie, mimośród jest zawsze liczbą mniejszą od jedności.

Ile ognisk ma elipsa?
Elipsa ma dwa ogniska.
Zadania z rozwiązaniami

Zadanie nr 1.
Jaka jest długość półosi wielkiej elipsy o równaniu \(x^2+16y^2=144\)? Sporządź szkic tej elipsy w układzie współrzędnych.

Zadanie nr 2.
Zaznaczyć w układzie współrzędnych ogniska elipsy o równaniu \(\frac{x^2}{4}+y^2=1\).

Zadanie nr 3.
Dana jest elipsa o równaniu \(x^2+4y^2=4\). Obliczyć mimośród tej elipsy.

Zadanie nr 4.
Dana jest elipsa o mimośrodzie \(\varepsilon=\frac{1}{2}\) i ognisku w punkcie \(F=(\frac{3}{2},0)\). Znaleźć równanie tej elipsy.
Powiązane materiały
 Elipsa
Elipsa© medianauka.pl, 2010-12-17, A-1054
Data aktualizacji artykułu: 2023-06-14

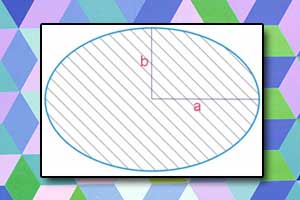 Pole i obwód elipsy
Pole i obwód elipsy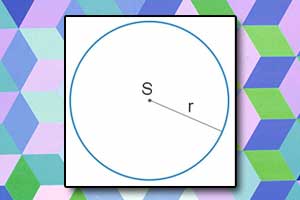 Okrąg i koło
Okrąg i koło