Pole i obwód elipsy

Mówiąc o polu powierzchni elipsy, mamy na myśli figurę geometryczną ograniczoną poprzez krzywą, która jest elipsą.

Pole elipsy

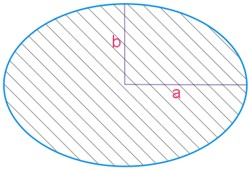
Twierdzenie

Pole powierzchni elipsy wyraża się wzorem:

\(P=\pi ab\)

Oznaczenia: \(a\) oraz \(b\) są półosiami elipsy.

Kalkulator

Pole elipsy — kalkulator
Podaj długość dwóch półosi elipsy, a nasz kalkulator obliczy pole powierzchni elipsy.

Wpisz dane:

Pierwsza półoś elipsy:

Druga półoś elipsy:

Rozwiązanie:

Obwód elipsy

Obwodu elipsy nie da się przedstawić w postaci algebraicznej. Stosujemy wzory przybliżone lub następujący wzór:

Twierdzenie

Obwód elipsy wyraża się wzorem:

\(L=4aE(\varepsilon)=2\pi a[1-(\frac{1}{2})^2\varepsilon ^2-(\frac{1\cdot 3}{2\cdot 4})^2 \cdot \frac{\varepsilon ^4}{3}-(\frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6})^2 \cdot \frac{\varepsilon ^6}{5}-...]\)

gdzie \(a\) jest wielką półosią elipsy, \(\varepsilon\) — mimośród elipsy, natomiast \(E(\varepsilon)\) jest pełną całką eliptyczną drugiego rodzaju (całka eliptyczna jest pojęciem z zakresu studiów wyższych, dlatego warto zapoznać się ze wzorem przybliżonym).

W literaturze można również znaleźć wiele wzorów przybliżonych. Oto jeden z nich:

\(L=\pi[\frac{3}{2}(a+b)-\sqrt{ab}]\)

Zadania z rozwiązaniami

Zadanie nr 1.

Oblicz pole powierzchni elipsy przedstawionej na rysunku.

Elipsa

Pokaż rozwiązanie zadania.

Zadanie nr 2.

Oblicz pole powierzchni elipsy, której półosie mają długości 6 i 5.

Pokaż rozwiązanie zadania.

Zadanie nr 3.

Oblicz pole powierzchni elipsy o równaniu \(2x^2+3y^2=6\).

Pokaż rozwiązanie zadania.

Zadanie nr 4.

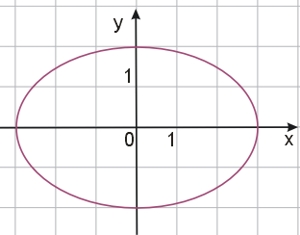
Dany jest okrąg o równaniu \(x^2+y^2=4\). Długość półosi wielkiej pewnej elipsy jest równa długości promienia okręgu. Pole tej elipsy jest dwa razy mniejsze od pola koła wyznaczonego przez okrąg. Jaka jest długość drugiej półosi elipsy?

Pokaż rozwiązanie zadania.

Zadanie nr 5.

Ile sznurka potrzeba do ułożenia elipsy o polu \(6\pi\) i osi wielkiej elipsy o długości 6.

Pokaż rozwiązanie zadania.

Inne zagadnienia z tej lekcji

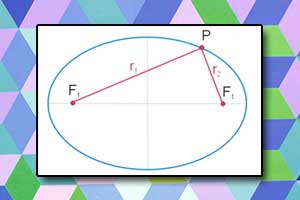Elipsa