Nauka » Matematyka » Pole i obwód elipsy

zadanie

Zadanie - obliczyć pole elipsy

Dany jest okrąg o równaniu

. Długość półosi wielkiej pewnej elipsy jest równa długości promienia okręgu. Pole tej elipsy jest dwa razy mniejsze od pola koła wyznaczonego przez okrąg. Jaka jest długość drugiej półosi elipsy?

Rozwiązanie zadania uproszczone

$P_k=\pi a^2=4\pi$
$P_e=\pi ab=2\pi b\\ P_e=\frac{1}{2}P_k=2\pi\\ 2\pi b=2\pi /:2\pi\\ b=1$

Rozwiązanie zadania ze szczegółowymi wyjaśnieniami

Równanie okręgu o środku O(x_s,y_s) ma następującą postać:

W naszym przypadku mamy więc:

$x^2+y^2=4\\ (x-0)^2+(y-0)^2=2^2\\ x_s=0, \ y_s=0, \ r=2$

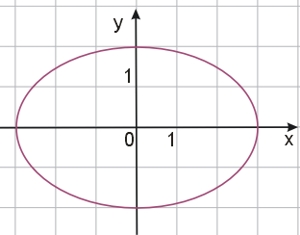
Równanie opisuje więc okrąg o środku w punkcie O(0,0) (początek układu współrzędnych) i promieniu r=0. Półoś wielka a=r=2. Oznaczmy półoś małą elipsy przez b. Jest to wielkość szukana. Sporządzamy szkic:

Elipsy

Pole elipsy obliczamy ze wzoru:

$P_e=\pi ab$

gdzie a,b to długości półosi elipsy.

Pole koła obliczamy ze wzoru:

$P_k=\pi r^2$

Z warunków zadania wiemy, że a=r, obliczamy więc pole koła:

$P_k=\pi r^2=\pi a^2=\pi \cdot 2^2=4\pi$ tło

Wiemy, że pole elipsy jest dwa razy mniejsze od pola koła. Obliczamy pole powierzchni elipsy:

$a=2\\ P_e=\pi ab=2\pi b\\ P_e=\frac{1}{2}P_k=\frac{1}{2}\cdot 4\pi=2\pi\\ 2\pi b=2\pi /:2\pi\\ b=1$ tło

Odpowiedź

© medianauka.pl, 2011-01-22, ZAD-1121

Zadania podobne

Zadanie - pole powierzchni elipsy
Oblicz pole powierzchni elipsy przedstawionej na rysunku.
Elipsa

Elipsa

Zadanie - pole elipsy
Oblicz pole powierzchni elipsy, której półosie mają długości 6 i 5.

Zadanie - pole elipsy, obliczanie pola powierzchni elipsy
Oblicz pole powierzchni elipsy o równaniu

Zadanie - oblicz obwód elipsy
Ile sznurka potrzeba do ułożenia elipsy o polu $6\pi$ i osi wielkiej elipsy o długości 6.

Logika i zbiory

Zbiory

Liczby

Liczby

Funkcje

Funkcje

Równania i nierówności

Równania

Analiza

Analiza

Geometria

Geometria

Prawdopodobieństwo

Probabilistyka

Polecamy

Zioła w leczeniu artretyzmu, reumatyzmu ...

Zioła w leczeniu artretyzmu, reumatyzmu ...
Mateusz E. Senderski

Prawda ostateczna. Jak odkryliśmy narodziny wszechświata

Prawda ostateczna. Jak odkryliśmy narodziny wszechświata
John Gribbin

Zioła w leczeniu chorób układu moczowo-płciowego

Zioła w leczeniu chorób układu moczowo-płciowego
Mateusz Emanuel Senderski

FEYNMANA WYKŁADY Z FIZYKI

FEYNMANA WYKŁADY Z FIZYKI
R.P. Feynman, R.B. Leighton, M. Sands

© Media Nauka 2008-2017 r.