Równoległobok
Co to jest równoległobok? Oto definicja równoległoboku.
Na poniższej ilustracji przedstawiono różne rodzaje równoległoboków.

Zauważmy, że kwadrat i prostokąt również jest równoległobokiem.
Wysokość równoległoboku
Wysokość równoległoboku jest to odcinek, który łączy dowolny wierzchołek równoległoboku z jego rzutem na bok lub jego przedłużenie, który (które) nie zawiera tego wierzchołka. Wysokość zwykle oznaczamy literką \(h\). Zgodnie z takim określeniem wysokości w równoległoboku, mamy dwie wysokości, które mogą mieć różną długość.
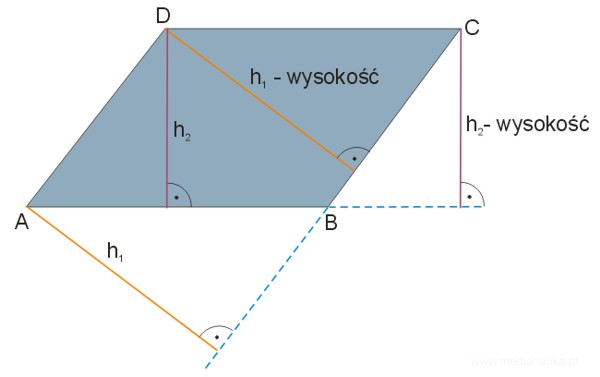
Jeżeli równoległobok ma wszystkie boki równe, to mamy do czynienia z rombem. Równoległobok, który ma wszystkie kąty proste, to prostokąt. Równoległobok, który jest prostokątem i ma wszystkie boki równe, to kwadrat.
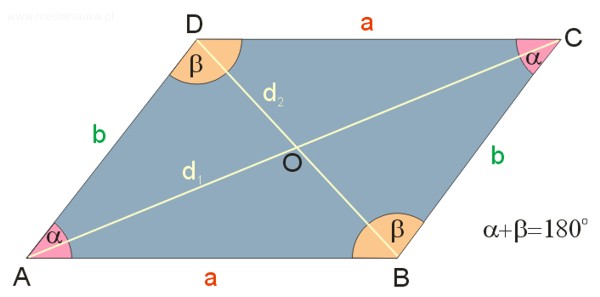
Własności równoległoboku
- Każdy równoległobok ma środek symetrii.
- Przekątne równoległoboku się połowią.
- Każde dwa boki przeciwległe równoległoboku są równe.
- Każde dwa kąty przeciwległe równoległoboku są równe.
- Suma miar każdych dwóch kątów, które leżą przy tym samym boku, jest równa 180°.
- Suma miar wszystkich kątów wewnętrznych równoległoboku jest równa 360°.
- Dwa przeciwległe boki są równe i równoległe.
Pole i obwód równoległoboku
W następnym artykule pokazujemy jak obliczyć pole powierzchni równoległoboku oraz jego obwód.
Pytania
Czy prostokąt jest równoległobokiem?
Równoległobok jest to czworokąt, który ma dwie pary boków równoległych. Zatem każdy prostokąt jest jednocześnie równoległobokiem. Jednak nie każdy równoległobok jest prostokątem.
Czy każdy równoległobok jest trapezem?
Trapez jest to czworokąt, który ma co najmniej jedną parę boków równoległych. Każdy równoległobok ma dwie pary boków równoległe, zatem każdy równoległobok jest także trapezem. Nie każdy trapez jest równoległobokiem.
Ile osi symetrii ma równoległobok?
Równoległobok, który nie jest prostokątem, nie ma osi symetrii. Ma jedynie środek symetrii. Jeżeli równoległobok jest prostokątem, ma wówczas dwie, a jeżeli kwadratem — cztery osie symetrii.
Zadania z rozwiązaniami

Zadanie nr 1 — maturalne.
W równoległoboku \(ABCD\), przedstawionym na rysunku, kąt α ma miarę 70°.
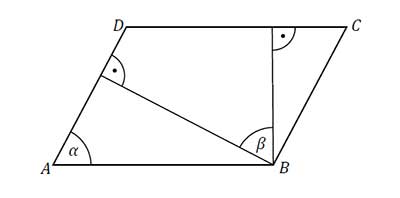
Wtedy kąt β ma miarę
A. 80°
B. 70°
C. 60°
D. 50°
Wybrane karty pracy
Powiązane materiały
© medianauka.pl, 2010-11-24, A-1025
Data aktualizacji artykułu: 2023-06-25


 Trapez
Trapez Pole i obwód trapezu
Pole i obwód trapezu Pole równoległoboku
Pole równoległoboku Romb
Romb Pole rombu
Pole rombu Deltoid
Deltoid Inne czworokąty
Inne czworokąty