Kąt
Definicja
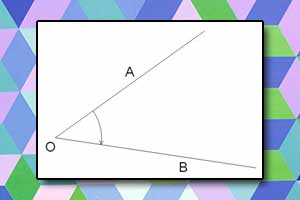
Kąt nieskierowany, kąt płaski, nazywany krótko kątem, jest to zbiór utworzony z dwóch różnych półprostych o wspólnym początku i jednej z figur, wyciętych z płaszczyzny przez te dwie półproste.
Półproste noszą nazwę ramion kąta, a ich wspólny początek, to wierzchołek kąta. Wnętrze kąta, to figura wycięta z płaszczyzny przez dwie półproste, natomiast obszar kąta, to wnętrze kąta wraz z dwoma półprostymi. Wszystkie pojęcia zostały zilustrowane poniższym rysunkiem.
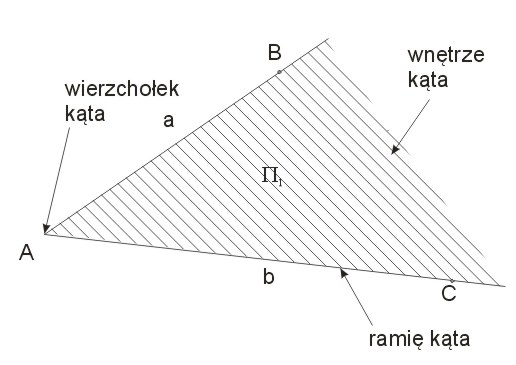
Zauważmy, że powyższą definicję spełnia także taki przypadek:
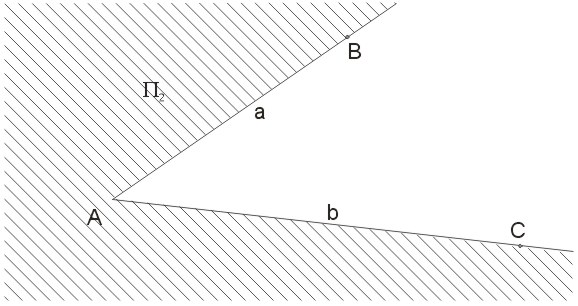
Dwie półproste wyznaczają więc na płaszczyźnie dwa kąty. Każdy z nich będziemy oznaczać tak samo:\(\angle{BAC}\), podając w środku punkt stanowiący wierzchołek kąta. Gdy posługujemy się takim oznaczeniem, dla odróżnienia od siebie obu kątów zwykle wskazujemy na dodatkowe informacje dotyczące danego kąta.
Jak oznaczamy kąty?
Do oznaczania kątów używamy także liter alfabetu greckiego: \(\alpha,\beta,\gamma,\delta,...\) (alfa, beta, gamma, delta itd.).
W praktyce na rysunkach kąty oznaczamy w inny sposób. Zamiast zaznaczać całe wnętrze kąta, zaznaczamy je poprzez narysowanie łuku. Ilustruje to poniższy rysunek:
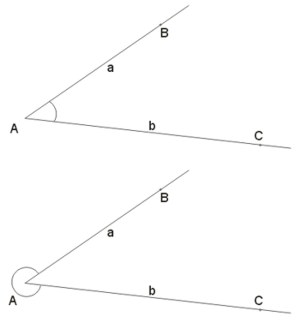
Kąt wypukły i wklęsły
W pierwszym przypadku mamy do czynienia z figurą wypukłą, a kąt nazywamy wypukłym. Na drugim rysunku mamy do czynienia z figurą niewypukłą, a taki kąt będziemy nazywać kątem wklęsłym.
Przypomnijmy, że kąt wypukły to taka figura, że każdy odcinek o końcach, należących do tej figury, zawiera się w tej figurze. Kąt wklęsły to taki kąt, który nie jest wypukły.
Przykłady
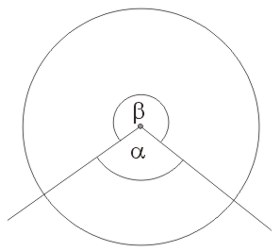
Na rysunku zaznaczono kilka kątów. Kąty \(\alpha, \gamma\) są kątami wypukłymi, natomiast kąt \(\beta\) jest kątem wklęsłym.
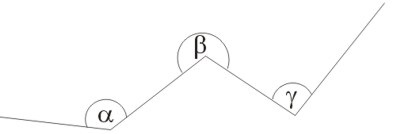
Rodzaje kątów
Rozróżniamy wiele rodzajów kątów. Tu wymieniamy wybrane z nich.
Kąt półpełny
Kąt półpełny jest to kąt, którego ramiona uzupełniają się do prostej.
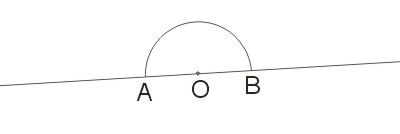
Kąt półpełny ma miarę 180° (\(\pi\) rad).
Kąt zerowy
Kąt zerowy jest to kąt, którego ramiona pokrywają się, a jego wnętrze jest puste.
Kąt zerowy ma miarę 0° (0 rad).
Kąt pełny
Kąt pełny jest to kąt, którego ramiona pokrywają się, a jego obszar pokrywa całą płaszczyznę.
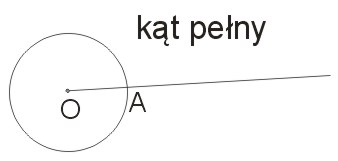
Kąt pełny ma miarę 360° (\(2\pi\) rad).
O kątach zerowym, półpełnym i pełnym nie mówimy, że są wypukłe.
Kąty w kole
Kąt środkowy
Kąt środkowy koła jest to kąt, którego wierzchołek jest środkiem tego koła.
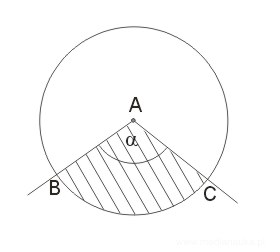
Wycinek kołowy
Wycinek kołowy jest to część wspólna koła i obszaru kąta środkowego.
Kąt wpisany w okrąg
Kąt wpisany w okrąg (w koło) jest to kąt wypukły, którego wierzchołek leży na okręgu, a ramiona przecinają okrąg w dwóch różnych punktach.
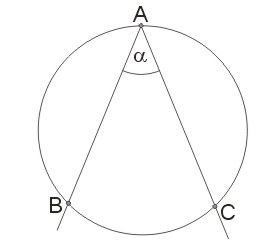
Punkty przecięcia ramion kąta z okręgiem wyznaczają cięciwę. O kącie mówimy wtedy, że jest oparty na tej cięciwie. Kąt wpisany w okrąg wyznacza łuk zawarty w tym kącie. Mówimy, że kąt jest oparty na tym łuku.
Kąty wierzchołkowe
Kąt wierzchołkowy do danego kąta wypukłego jest to kąt wypukły, którego ramiona są przedłużeniem ramion danego kąta.
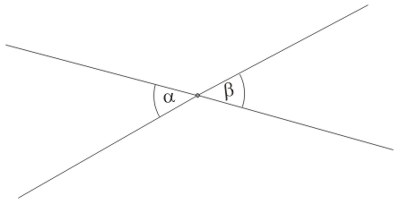
Twierdzenie
Kąty przyległe
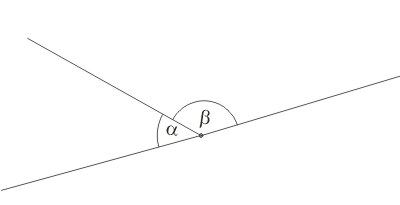
Kąt przyległy do danego kąta wypukłego jest to kąt wypukły, który ma z danym kątem jedno ramię wspólne, a którego drugie ramię jest przedłużeniem drugiego ramienia danego kąta.
Kąty dopełniające
Kąty dopełniające to kąty, których suma jest katem prostym.
W geometrii Euklidesa w trójkącie prostokątnym trójkąty ostre są trójkątami dopełniającymi.
Kąt prosty
Kąt prosty jest to kąt równy kątowi do niego przyległemu. Kąty proste oznaczamy kropką (ja na rysunku poniżej).
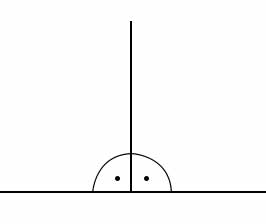
Kąt prosty ma miarę 90° (\(\frac{\pi}{2}\) rad).
Kąt rozwarty
Kąt rozwarty jest to każdy kąt wypukły, który jest większy od kąta prostego i mniejszy od kąta półpełnego.
Ile stopni ma kąt rozwarty? Kąt rozwarty ma miarę większą od 90° (\(\frac{\pi}{2}\) rad) i mniejszą od 180° (\(\pi\) rad).
Kąt ostry
Kąt ostry jest to każdy kąt wypukły, który jest mniejszy od kąta prostego i większy od kąta zerowego.
Ile stopni ma kąt ostry? Kąt ostry ma miarę większą od 0° i mniejszą od 90° (\(\frac{\pi}{2}\) rad).
Pytania
Co to jest kąt nieskierowany?
Na to pytanie odpowiadamy w następnym artykule.
Co to jest kąt dwuścienny?
Na to pytanie odpowiadamy tutaj.
Zadania z rozwiązaniami

Zadanie nr 1 — maturalne.
Kąt środkowy oparty na łuku, którego długość jest równa \(\frac{4}{9}\) długości okręgu, ma miarę:
A. \(160°\)
B. \(80°\)
C. \(40°\)
D. \(20°\)

Zadanie nr 2 — maturalne.
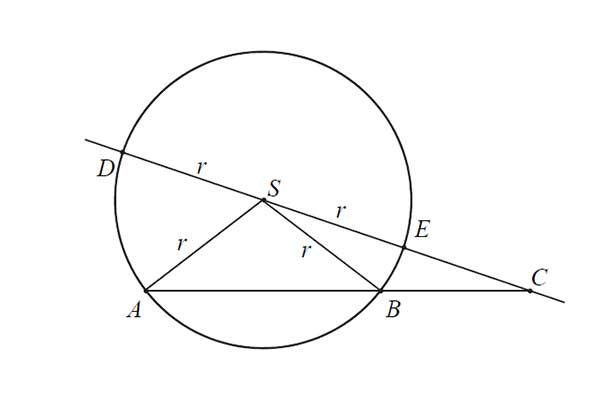
Dany jest okrąg o środku w punkcie \(S\) i promieniu \(r\). Na przedłużeniu cięciwy \(AB\) poza punkt \(B\) odłożono odcinek \(BC\) równy promieniowi danego okręgu. Przez punkty \(C\) i \(S\) poprowadzono prostą. Prosta \(CS\) przecina dany okrąg w punktach \(D\) i \(E\) (zobacz rysunek). Wykaż, że jeżeli miara kąta \(ACS\) jest równa \(\alpha\), to miara kąta \(ASD\) jest równa \(3\alpha\).
Wybrane karty pracy
Powiązane materiały
 Kąty
Kąty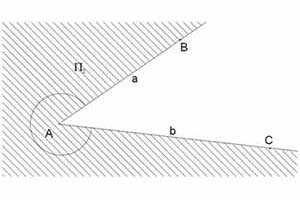 Kąty — quiz
Kąty — quiz© medianauka.pl, 2010-10-30, A-997
Data aktualizacji artykułu: 2023-06-10

 Kąt skierowany
Kąt skierowany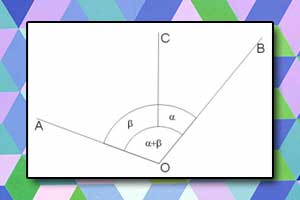 Miary kątów
Miary kątów Dwusieczna kąta
Dwusieczna kąta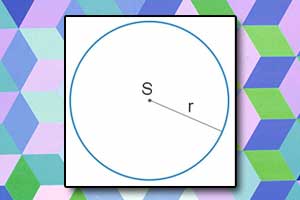 Okrąg i koło
Okrąg i koło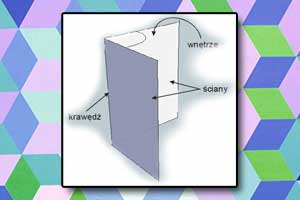 Kąt dwuścienny i wielościenny
Kąt dwuścienny i wielościenny Kąty i ich miary — quiz
Kąty i ich miary — quiz