Kąt dwuścienny

Kąt dwuścienny jest to figura geometryczna utworzona przez dwie różne półpłaszczyzny o wspólnej krawędzi i jedną z dwóch figur wyciętych w przestrzeni przez te dwie półpłaszczyzny.

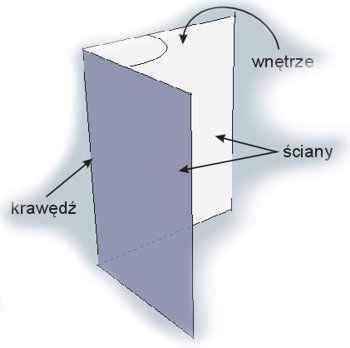
Dwie półpłaszczyzny wyznaczające kąt dwuścienny to ściany tego kąta, natomiast część wspólna obu płaszczyzn to krawędź kąta dwuściennego. Wnętrze kata dwuściennego to figura wycięta z przestrzeni przez ściany kata dwuściennego. Suma ścian i wnętrza kąta dwuściennego to jego obszar.

Kąt dwuścienny półpełny to taki kąt dwuścienny, którego ściany uzupełniają się do jednej płaszczyzny.

Kąt dwuścienny zerowy to taki kąt dwuścienny, którego ściany pokrywają się, a wnętrze jest puste.

Kąt dwuścienny pełny, to taki kąt dwuścienny, którego ściany pokrywają się, a wnętrze wypełnia całą przestrzeń.

Miarę kąta płaskiego, otrzymanego przez przecięcie kąta dwuściennego płaszczyzną prostopadłą do jego krawędzi nazywamy miarą kąta dwuściennego.

Kąt wielościenny

Dany jest ciąg \(n\) półprostych \(WA_1^{\rightarrow},\ WA_2^{\rightarrow},\ WA_3^{\rightarrow},...,WA_n^{\rightarrow},n\geq 3\) takich, że:

• Punkt W jest wspólnym początkiem wszystkich półprostych.
• Żadne z trzech półprostych nie leżą w jednej płaszczyźnie.
• Jeżeli \(\delta\) oznacza jedną z płaszczyzn \(WA_1A_2,\ WA_2A_3,...,\ WA_{n-1}A_n,...,WA_nA_1\) to wszystkie półproste zawierają się w jednej półprzestrzeni domkniętej o płaszczyźnie brzegowej \(\delta\).

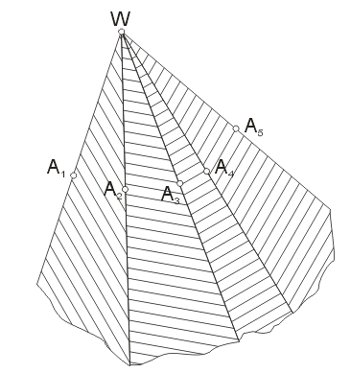
Ciąg tych półprostych nazywamy kątem wielościennym. Półproste nazywamy krawędziami tego kąta, a ich wspólny początek, to wierzchołek kąta wielościennego. Iloczyn n półprzestrzeni domkniętych opisanych w powyższym warunku (nr 3) jako półprzestrzenie o płaszczyznach brzegowych zawierających wszystkie krawędzie jest figurą wypukłą i nazywamy obszarem kąta wielościennego. Obszary kątów wypukłych \(\angle A_1WA_2,\angle A_2WA_3,...,\angle A_{n-1}WA_n,...,\angle A_nWA_1\) nazywamy ścianami kąta wielościennego.

Kąt wielościenny nie jest bryłą, gdyż nie jest figurą ograniczoną.

Powiązane materiały

Bryła

Proste prostopadłe w przestrzeni

Objętość

Stereometria — podstawy

Dwusieczna kąta

Kąt

© medianauka.pl, 2011-07-31, A-1395
Data aktualizacji artykułu: 2023-06-30