Proste prostopadłe w przestrzeni

Dwie proste w przestrzeni są prostopadłe, jeżeli dowolny wektor niezerowy zawarty w jednej prostej i dowolny wektor niezerowy w drugiej prostej tworzą kąt prosty.

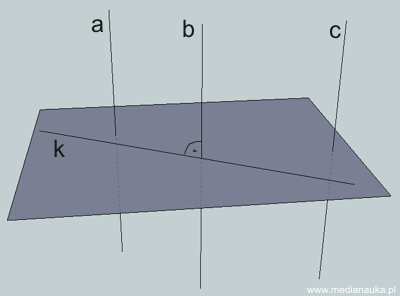
Zauważ, że prostopadłość prostych w przestrzeni różni się od prostopadłości prostych na płaszczyźnie, gdyż w przestrzeni dwie proste prostopadłe nie muszą się wcale przecinać. Ilustruje to poniższy rysunek.

Proste \(a, b, c\) są prostopadłe do \(k\), ale tylko prosta \(b\) przecina \(k\).

prostopadłość w przestrzeni

Prosta w przestrzeni jest prostopadła do płaszczyzny, jeżeli jest prostopadła do każdej prostej zawartej w tej płaszczyźnie.

Twierdzenie

Jeżeli prosta \(k\) jest prostopadła do prostych przecinających się \(a, b\) zawartych w pewnej płaszczyźnie, to prosta \(k\) jest prostopadła do tej płaszczyzny.

Inne zagadnienia z tej lekcji

Bryła

Kąt dwuścienny i wielościenny

Objętość

Stereometria — podstawy

Proste prostopadłe

Wzajemne położenie prostych