Proste prostopadłe
Co to jest prosta prostopadła do prostej?
Definicja
Prostą \(a\) nazywamy prostopadłą do prostej \(b\), jeżeli prosta \(b\) jest osią symetrii prostej \(a\) i jest od niej różna.
Proste prostopadłe oznaczamy następującym symbolem: \(a\perp b\).
Konstrukcja prostej prostopadłej
Jak narysować prostą prostopadłą? Pokażemy dwa sposoby konstrukcji prostej prostopadłej.
Sposób 1.
Poniższy film pokazuje sposób konstrukcji prostej prostopadłej do prostej \(a\), przechodzącej przez punkt \(X\), który leży poza prostą \(a\).
Sposób 2.
Poniższy film pokazuje sposób konstrukcji prostej prostopadłej do prostej \(a\), przechodzącej przez punkt \(X\), który leży na prostej \(a\).
Twierdzenia o prostych prostopadłych
- Dwie proste prostopadłe do trzeciej prostej są równoległe.
- Jeżeli z dwóch prostych równoległych jedna jest prostopadła do trzeciej prostej, to i ta druga prosta jest prostopadła do tej trzeciej prostej.
- Jeżeli dwie proste przecinają się, to proste prostopadłe do tych prostych również się przecinają.
- Jeśli jedna z dwóch prostych jest prostopadła do trzeciej prostej, a druga nie jest prostopadła do tej trzeciej prostej, to te dwie proste nie są równoległe.
Badanie, czy proste są prostopadłe na podstawie danych równań prostych, zostało omówione w artykule Wzajemne położenie prostych na płaszczyźnie.
Równanie prostej prostopadłej
Dwie proste na płaszczyźnie są prostopadłe, jeżeli współczynnik kierunkowy jednej prostej jest odwrotnością drugiego współczynnika kierunkowego ze znakiem minus, czyli:
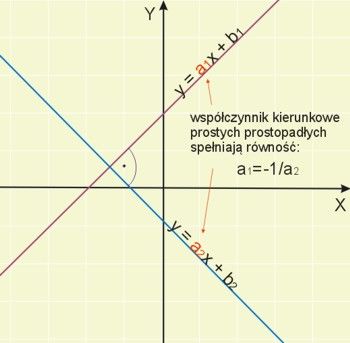
Przykłady
Zadania z rozwiązaniami

Zadanie nr 1 — maturalne.
Proste opisane równaniami \(y=\frac{2}{m-1}x+m-2\) oraz \(y=mx+\frac{1}{m+1}\) są prostopadłe, gdy:
A. \(m=2\)
B. \(m=\frac{1}{2}\)
C. \(m=\frac{1}{3}\)
D. \(m=-2\)

Zadanie nr 2 — maturalne.
W kartezjańskim układzie współrzędnych \((x,y)\) dane są proste \(k\) oraz \(l\) o równaniach
\(k: y=\frac{2}{3}x\)
\(l: y=-\frac{3}{2}x+13\)
Dokończ zdanie. Wybierz odpowiedź \(A\) albo B oraz odpowiedź 1., 2. albo 3.
Proste \(k\) oraz \(l\) są
A. prostopadłe
B. nie sąprostopadłe
i przecinają się w punkcie \(P\) o współrzędnych
1. \((−6,−4)\)
2. \((6,4)\)
3. \((−6,4)\)
Powiązane materiały
© medianauka.pl, 2010-11-07, A-1006
Data aktualizacji artykułu: 2023-06-06

 Proste równoległe
Proste równoległe Pole figury
Pole figury Proste prostopadłe i równoległe, pole
Proste prostopadłe i równoległe, pole Proste prostopadłe w przestrzeni
Proste prostopadłe w przestrzeni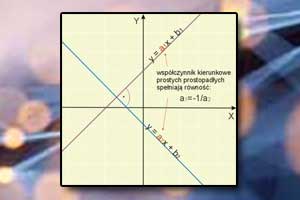 Wzajemne położenie prostych
Wzajemne położenie prostych