Wzajemne położenie prostych
Wzajemne położenie prostych na płaszczyźnie zależy od ich współczynników kierunkowych.
Jeżeli znamy równania opisujące dwie proste na płaszczyźnie, to bez konieczności szkicowania ich wykresów możemy stwierdzić, czy proste te są równoległe, prostopadłe, czy też przecinają się ze sobą pod pewnym kątem.
Proste równoległe
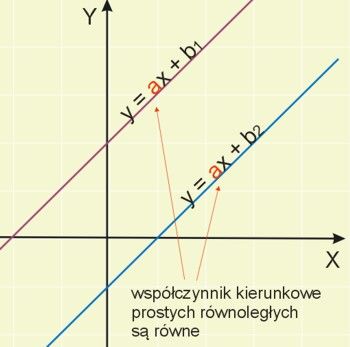
Dwie proste na płaszczyźnie są równoległe, jeżeli mają równe współczynniki kierunkowe \(a\), czyli \(a_1=a_2\) — to wzór na współczynnik kierunkowy prostej równoległej.
Równanie prostej równoległej
Jeżeli dana jest prosta o równaniu \(y=a_1x+b_1\), to równanie prostej równoległej jest następujące:
Przykłady
Dwie proste \(y=-3x-7, y=-3x+\frac{1}{2}\) są równoległe, ponieważ mają taki sam współczynnik kierunkowy prostej \(a=-3\).
Proste prostopadłe
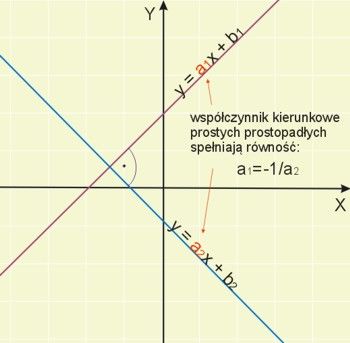
Kiedy proste są prostopadłe? Dwie proste na płaszczyźnie są prostopadłe, jeżeli współczynnik kierunkowy jednej prostej jest odwrotnością drugiego współczynnika kierunkowego ze znakiem minus, czyli \(a_1=-\frac{1}{a_2}\) — to wzór na współczynnik kierunkowy prostej prostopadłej.
Równanie prostej prostopadłej
Jeżeli dana jest prosta o równaniu \(y=a_1x+b_1\), to równanie prostej prostopadłej jest następujące:
Przykłady
Dwie proste \(y=-3x-7,y=-3x+\frac{1}{2}\) są względem siebie prostopadłe, ponieważ \(a_1=-3, a_2=\frac{1}{3}, a_1=-\frac{1}{a_2}\).
Rozpatrywaliśmy do tej pory proste prostopadłe i równoległe.
W pozostałych przypadkach proste przecinają się pod pewnym kątem różnym od kąta prostego.
Kiedy współczynniki kierunkowe prostych oraz wyrazy wolne są takie same, to mamy do czynienia z prostymi równoległymi pokrywającymi się (nieskończenie wiele punktów przecięcia się).
Prosta prostopadła przechodząca przez punkt
Jak znaleźć równanie prostej prostopadłej do danej, która przechodzi przez dany punkt? Najlepiej pokazać to na przykładzie:
Przykłady
Dana jest prosta o równaniu \(y=-\frac{1}{2}x+6\). Wyznacz równanie prostej prostopadłej do niej, która przechodzi przez punkt \(A=(4,6)\).
Równanie prostej prostopadłej będzie dane wzorem:
\(y=-\frac{1}{-\frac{1}{2}}x+b_2\)
\(y=2x+b_2\)
Podstawiamy za \(x, y\) współrzędne punktu \(A\).
\(6=2\cdot 4+b_2\)
\(6=8+b_2\)
\(b_2=-2\)
Zatem równanie szukanej prostej jest następujące: \(y=2x-2\).
Odległość między prostymi równoległymi
Odległość między dwiema prostymi równoległymi, które określone są równaniami w postaci ogólnej \(Ax+By+C=0\) i \(Ax+By+C_1=0\), gdzie \(A^2+B^2\neq 0\) jest wyrażona wzorem:
Przykład
Policzymy odległość między prostymi \(y=2x+1\) i \(y=2x-4\).
Sprowadzamy najpierw oba równania do postaci ogólnej:
\(-2x+y-1=0\) i \(-2x+y+4=0\)
Obliczamy odległość między tymi prostymi wprost ze wzoru:
\(d=\frac{|4+1|}{\sqrt{(-2)^2+1^2}}=\frac{5}{\sqrt{5}}=\sqrt{5}\)
Pytania
Jak skonstruować prostą równoległą?
Wyjaśniamy to na filmie w artykule proste równoległe.
Jak skonstruować prostą prostopadłą?
Wyjaśniamy to na filmie w artykule proste prostopadłe.
Zadania z rozwiązaniami
Zadanie nr 1 — maturalne.
Proste o równaniach: \(y=2mx-m^2-1\) oraz \(y=4m^2x+m^2+1\) są prostopadłe dla:
A. \(m=-\frac{1}{2}\)
B. \(m=\frac{1}{2}\)
C. \(m=1\)
D. \(m=2\)
Zadanie nr 2 — maturalne.
W kartezjańskim układzie współrzędnych \((x,y)\) dana jest prosta \(k\) o równaniu \(y=-\frac{1}{3}x+2\). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Prosta o równaniu \(y=ax+b\) jest równoległa do prostej \(k\) i przechodzi przez punkt \(P=(3,5)\), gdy
A. \(a=3, b=4\)
B. \(a=-\frac{1}{3}, b=4\)
C. \(a=3, b=-4\)
D. \(a=-\frac{1}{3}, b=6\)
Zadanie nr 3 — maturalne.
Dane są cztery proste k, l, m o równaniach:
\(k: y=-x+1\)
\(l: y=\frac{2}{3}x+1\)
\(m: y=-\frac{3}{2}x+4\)
\(n: y=-\frac{2}{3}x-1\)
Wśród tych prostych prostopadłe są
A. proste k oraz l.
B. proste k oraz n.
C. proste l oraz m.
D. proste m oraz n.
Zadanie nr 4 — maturalne.
Na rysunku obok przedstawiono geometryczną interpretację jednego z niżej zapisanych układów
Proste o równaniach \(y=3x-5\) oraz \(y=\frac{(m-3)}{2}+\frac{9}{2}\) są równoległe, gdy
A. \(m=1\)
B. \(m=3\)
C. \(m=6\)
D. \(m=9\)
Zadanie nr 5 — maturalne.
Proste o równaniach \(y=(m−2)x\) oraz \(y=\frac{3}{4}x+7\) są równoległe. Wtedy
A. \(m=-\frac{5}{4}\)
B. \(m=\frac{2}{3}\)
C. \(m=\frac{11}{4}\)
D. \(m=\frac{10}{3}\)
Zadanie nr 6 — maturalne.
Prosta o równaniu \(y=ax+b\) jest prostopadła do prostej o równaniu \(y=− 4x+1\) i przechodzi przez punkt \(P=(\frac{1}{2},0)\), gdy
A. \(a=-4\) i \(b=-2\)
B. \(a=\frac{1}{4}\) i \(b=-\frac{1}{8}\)
C. \(a=-4\) i \(b=2\)
D. \(a=\frac{1}{4}\) i \(b=\frac{1}{2}\)
Zadanie nr 7 — maturalne.
Proste o równaniach \(y=(2m+2)x−2019\) oraz \(y=(3m−3)x+2019\) są równoległe, gdy
A. \(m=-1\)
B. \(m=0\)
C. \(m=1\)
D. \(m=5\)
Zadanie nr 8 — maturalne.
W układzie współrzędnych punkty \(A=(4,3)\) i \(B=(10,5)\) są wierzchołkami trójkąta ABC. Wierzchołek \(C\) leży na prostej o równaniu \(y=2x+3\). Oblicz współrzędne punktu \(C\), dla którego kąt \(ABC\) jest prosty.
Zadanie nr 9 — maturalne.
Odległość początku układu współrzędnych od prostej o równaniu \(y = 2x + 4\) jest równa
A. \(\frac{\sqrt{5}}{5}\)
B. \(\frac{4\sqrt{5}}{5}\)
C. \(\frac{4}{5}\)
D. \(4\)
Zadanie nr 10.
Dana jest prosta o równaniu \(y=-7x+5\). Znaleźć równanie prostej równoległej do tej prostej, przechodzącej przez początek układu współrzędnych.
Zadanie nr 11 — maturalne.
Prosta l o równaniu \(y=m^2x+3\) jest równoległa do prostej k o równaniu \(y=(4m-4)x-3\). Zatem:
A. \(m=2\)
B. \(m=-2\)
C. \(m=-2-2\sqrt{2}\)
D. \(m=-2+2\sqrt{2}\)
Zadanie nr 12 — maturalne.
Punkty \(A=(30,32)\) i \(B=(0,8)\) są sąsiednimi wierzchołkami czworokąta \(ABCD \) wpisanego w okrąg. Prosta o równaniu \(x-y+2=0\) jest jedyną osią symetrii tego czworokąta i zawiera przekątną \(AC\). Oblicz współrzędne wierzchołków \(C\) i \(D\) tego czworokąta.
Zadanie nr 13 — maturalne.
Proste opisane równaniami \(y=\frac{2}{m-1}x+m-2\) oraz \(y=mx+\frac{1}{m+1}\) są prostopadłe, gdy:
A. \(m=2\)
B. \(m=\frac{1}{2}\)
C. \(m=\frac{1}{3}\)
D. \(m=-2\)
Zadanie nr 14.
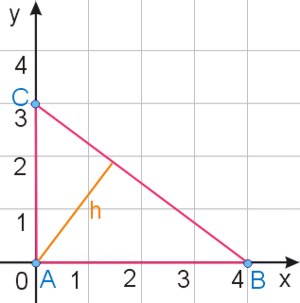
Znaleźć równanie prostej, która zawiera wysokość w trójkącie \(ABC\) przedstawionym na poniższym rysunku:
Zadanie nr 15.
Znaleźć równania wszystkich prostych prostopadłych przechodzących przez punkty \(A(1,2), B(2,-1), C(-1,3)\).
Zadanie nr 16.
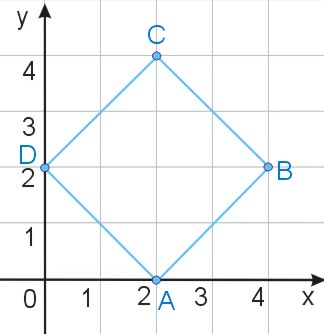
Znaleźć równania prostych zawierających boki kwadratu ABCD, jeśli wiadomo, że współrzędne wierzchołków są liczbami całkowitymi.
Zadanie nr 17.
Dana jest prosta o równaniu \(y=5x+\frac{1}{5}\). Znaleźć równanie prostej prostopadłej do tej prostej, przechodzącej przez punkt \(A(1,-1)\).
Powiązane materiały
Funkcja liniowa
Wykres funkcji liniowej
Funkcja liniowa
Proste prostopadłe w przestrzeni
Proste prostopadłe
Proste równoległe
Proste równoległe i prostopadłe
Funkcja liniowa — quiz© medianauka.pl, 2009-06-21, A-237
Data aktualizacji artykułu: 2023-04-15