Funkcja liniowa
Funkcja liniowa jest to funkcja określona wzorem:
Litery \(a\) i \(b\) oznaczają dowolne liczby rzeczywiste. Liczby te posiadają swoje nazwy:
\(a\) — jest to współczynnik kierunkowy prostej lub współczynnik kierunkowy funkcji liniowej,
\(b\) — jest to wyraz wolny.
Powyższy wzór jest to wzór funkcji liniowej lub postać ogólna funkcji liniowej.
Wzór ogólny funkcji liniowej:
\(y=ax+b,\quad{x}\in{R}\)
Wzór na miejsce zerowe funkcji liniowej: \(x_0=-\frac{b}{a}\)
Przykłady funkcji liniowej
Oto kilka przykładów funkcji liniowych:
- Funkcja \(y=5x+1\), współczynnik kierunkowy prostej \(a=5\), wyraz wolny \(b=1\).
- Funkcja \(y=16x\), współczynnik kierunkowy prostej \(a=16\), wyraz wolny \(b=0\).
- Funkcja \(y=-x+2\), współczynnik kierunkowy prostej \(a=-1\), wyraz wolny \(b=2\).
- Funkcja \(y=1\), współczynnik kierunkowy prostej \(a=0\), wyraz wolny \(b=1\).
Własności funkcji liniowej
Oto wybrane własności funkcji liniowej:
Dziedzina i zbiór wartości funkcji liniowej
Dziedziną funkcji liniowej jest zbiór liczb rzeczywistych \(\mathbb{R}\).
Przeciwdziedziną funkcji liniowej, czyli zbiorem wartości funkcji jest:
- Dla \(a\neq 0\) przeciwdziedziną funkcji liniowej jest zbiór liczb rzeczywistych \(\mathbb{R}\);
- Dla \(a=0\) przeciwdziedziną funkcji liniowej jest zbiór jednoelementowy \(\lbrace b\rbrace\) (gdzie \(b\) to wyraz wolny).
Monotoniczność funkcji liniowej
- Funkcja liniowa jest rosnąca w całej swej dziedzinie, jeżeli \(a>0\).
- Funkcja liniowa jest malejąca w całej swej dziedzinie, jeżeli \(a<0\).
- Funkcja liniowa jest stała w całej swej dziedzinie, jeżeli \(a=0\).
Dowód
Udowodnimy pierwsze i drugie twierdzenie.
Wybieramy dwa dowolne argumenty \(x_1, x_2\) takie, że \(x_1<x_2\), czyli: \(x_1- x_2< 0\). Sprawdzimy jak się zachowują wartości funkcji dla tych argumentów. Obliczmy więc wartości funkcji:
\(f(x_1)=ax_1+b\)
\(f(x_2)=ax_2+b\)
Obliczamy różnicę wartości funkcji: \(f(x_1)-f(x_2)=ax_1+b-(ax_2+b)=ax_1-ax_2-a(x_1-x_2)\).
Z założenia wynika, że \(x_1- x_2< 0\), więc powyższy iloczyn jest mniejszy od zera, gdy \(a>0\) i wówczas mamy do czynienia z funkcją rosnącą (bo gdy rosną argumenty funkcji, rosną też wartości funkcji).
Mamy tutaj więc \(f(x_1)-f(x_2)= a(x_1-x_2)<0\) , zatem \(f(x_1)<f(x_2)\).
Natomiast gdy \(a<0\) mamy: \(f(x_1)-f(x_2)= a(x_1-x_2)>0\) (iloczyn dwóch liczb ujemnych jest dodatni) zatem \(f(x_1)>f(x_2)\) i mamy do czynienia z funkcją malejącą (dla rosnących argumentów funkcji maleją wartości funkcji).
(Jeżeli nie zrozumiałeś toku myślowego w powyższym postępowaniu, zapoznaj się z artykułem, dotyczącym badaniu monotoniczności funkcji.)
Miejsce zerowe funkcji liniowej
Poniżej wyjaśniamy jak obliczyć miejsce zerowe funkcji liniowej.
Funkcja liniowa:
- ma jedno miejsce zerowe gdy \(a\neq 0\), równe \(x_0=-\frac{b}{a}\),
- nie ma miejsc zerowych gdy \(a=0\) i \(b\neq 0\),
- ma nieskończenie wiele miejsc zerowych dla \(a=0\) i \(b=0\).
Przykłady
Wyznacz wzór funkcji liniowej, której wykres przechodzi przez punkty \(A=(1,2)\) i \(B=(3,9)\).
Gdy dane są dwa punkty, które należą do wykresu funkcji liniowej, wyznaczanie wzoru funkcji liniowej sprowadza się do rozwiązania układ równań. Podstawiając do równania \(y=ax+b\) za \(x\) i \(y\) odpowiednie współrzędne danych punktów wyliczamy \(a\) i \(b\).
\(\begin{cases} 2=a\cdot 1 +b\\ 9=a\cdot 3+b\end{cases}\)
Odejmując drugie równanie od pierwszego, otrzymamy:
\(7=2a/:2\)
\(a=\frac{7}{2}\)
\(b=2-\frac{7}{2}=-\frac{3}{2}\)
Wzór szukanej funkcji liniowej to \(y=\frac{7}{2}x-\frac{3}{2}\).
A oto inny przykład.
Przykłady
Jakie własności ma funkcja \(y=\frac{1}{2}x-6\)?
- Dziedziną tej funkcji jest zbiór liczb rzeczywistych \(\mathbb{R}\).
- Zbiorem wartości tej funkcji jest zbiór liczb rzeczywistych \(\mathbb{R}\).
- Funkcja jest rosnąca w całej swej dziedzinie (bo współczynnik kierunkowy jest dodatni).
- Miejscem zerowym tej funkcji jest \(x_0=-\frac{b}{a}=-\frac{-6}{\frac{1}{2}}=12\).
Jakie własności ma funkcja \(y=-x+1\)?
- Dziedziną tej funkcji jest zbiór liczb rzeczywistych \(\mathbb{R}\).
- Zbiorem wartości tej funkcji jest zbiór liczb rzeczywistych \(\mathbb{R}\).
- Funkcja jest malejąca w całej swej dziedzinie (bo współczynnik kierunkowy jest ujemny).
- Miejscem zerowym tej funkcji jest \(x_0=-\frac{b}{a}=-\frac{1}{-1}=1\).
Jakie własności ma funkcja \(y=1\)?
- Dziedziną tej funkcji jest zbiór liczb rzeczywistych \(\mathbb{R}\).
- Zbiorem wartości tej funkcji jest zbiór jednoelementowy \(\lbrace 1 \rbrace\).
- Funkcja jest stała w całej swej dziedzinie (bo współczynnik kierunkowy jest równy zero).
- Funkcja nie ma miejsc zerowych.
Kalkulator

Kalkulator — funkcja liniowa
Wpisz wzór funkcji liniowej, podając współczynniki \(a\) i \(b\) we wzorze \(y=ax+b\):
y= x+Pytania
Czy \(x=1\) jest wzorem funkcji liniowej?
Nie. To nawet nie jest funkcja.
Zadania z rozwiązaniami

Zadanie nr 2 — maturalne.
Dana jest funkcja liniowa \(f(x)=\frac{3}{4}x+6\). Miejscem zerowym tej funkcji jest liczba:
A. \(8\)
B. \(6\)
C. \(-6\)
D. \(-8\)

Zadanie nr 3 — maturalne.
Na wykresie funkcji liniowej określonej wzorem \(f(x)=(m-1)x+3\) leży punkt \(S=(5,-2)\). Zatem:
A. \(m=-1\)
B. \(m=0\)
C. \(m=1\)
D. \(m=2\)

Zadanie nr 4 — maturalne.
Funkcja liniowa f określona wzorem \(f(x)=2x+b\) ma takie samo miejsce zerowe, jakie ma funkcja liniowa \(g(x)=-3x+4\). Stąd wynika, że
A. \(b=4\)
B. \(b=-\frac{3}{2}\)
C. \(b=-\frac{8}{3}\)
D. \(b=\frac{4}{3}\)

Zadanie nr 5 — maturalne.
Funkcja liniowa \(f(x)=(m^2-4)x+2\) jest malejąca, gdy:
A. \(m\in [-2,2]\)
B. \(m\in (-2,2)\)
C. \(m\in (-\infty,2]\)
D. \(m\in [2,+\infty)\)

Zadanie nr 6 — maturalne.
O funkcji liniowej \(f\) wiadomo, że \(f(1)=2\). Do wykresu tej funkcji należy punkt \(P=(-2,3)\). Wzór funkcji \(f\) to:
A. \(f(x)=-\frac{1}{3}x+7/3\)
B. \(f(x)=-\frac{1}{2}x+2\)
C. \(f(x)=-3x+7\)
D. \(f(x)=-2x+4\)

Zadanie nr 7 — maturalne.
Funkcja liniowa \(f\) określona jest wzorem \(f(x)=\frac{1}{3}x-1\), dla wszystkich liczb rzeczywistych \(x\). Wskaż zdanie prawdziwe.
- Funkcja \(f\) jest malejąca i jej wykres przecina oś \(Oy\) w punkcie \(P=(0,\frac{1}{3})\).
- Funkcja \(f\) jest malejąca i jej wykres przecina oś \(Oy\) w punkcie \(P=(0,-1)\).
- Funkcja \(f\) jest rosnąca i jej wykres przecina oś \(Oy\) w punkcie \(P=(0,\frac{1}{3})\).
- Funkcja \(f\) jest rosnąca i jej wykres przecina oś \(Oy\) w punkcie \(P=(0,-1)\).

Zadanie nr 8 — maturalne.
Liczba \(1\) jest miejscem zerowym funkcji liniowej \(f(x)=ax+b\), a punkt \(M=(3,−2)\) należy do wykresu tej funkcji. Współczynnik \(a\) we wzorze tej funkcji jest równy
- \(1\)
- \(\frac{3}{2}\)
- \(-\frac{3}{2}\)
- \(-1\)

Zadanie nr 9 — maturalne.
Na rysunku przedstawiono fragment wykresu funkcji liniowej \(f\) określonej wzorem \(f(x)=ax+b\).
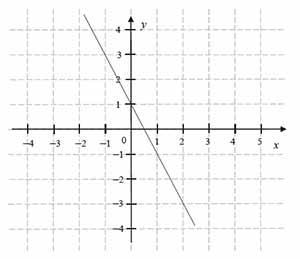
A. \(a+b>0\)
B. \(a+b=0\)
C. \(a\cdot b>0\)
D. \(a\cdot b<0\)
Powiązane materiały
 Funkcja liniowa
Funkcja liniowa© medianauka.pl, 2009-05-28, A-221
Data aktualizacji artykułu: 2023-04-10

 Wykres funkcji liniowej
Wykres funkcji liniowej Wzajemne położenie prostych
Wzajemne położenie prostych Funkcja liniowa
Funkcja liniowa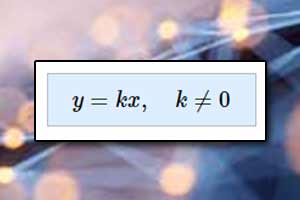 Proporcjonalność prosta
Proporcjonalność prosta Funkcja liniowa — quiz
Funkcja liniowa — quiz