Proporcjonalność prosta
Szczególnym przypadkiem funkcji liniowej, w którym wyraz wolny jest równy zeru, jest proporcjonalność prosta. Proporcjonalność prosta wyraża się zatem wzorem:
Liczbę \(k\) nazywamy współczynnikiem proporcjonalności prostej.
Wykres proporcjonalności prostej
Wykresem proporcjonalności prostej jest prosta przechodząca przez początek układu współrzędnych.
Na poniższym rysunku pokazano wykres proporcjonalności prostej \(y=3x\).
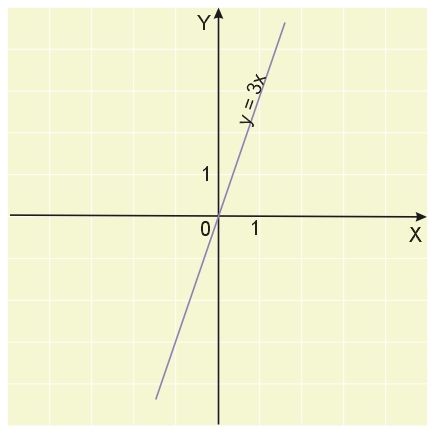
Z proporcjonalności prostej wynika, że \(\frac{y}{x}=k=const\).
Zapis const oznacza stałą liczbę (jest to skrót od słowa constans).
Oznacza to, że iloraz wartości funkcji i argumentu nie zmienia się, jest stały. Mówimy, że \(y\) jest wprost proporcjonalny do \(x\).
Przykłady
Długość przekątnej w kwadracie jest równa \(l=a\sqrt{2}\). Możemy powiedzieć, że długość przekątnej w kwadracie jest wprost proporcjonalna do długości boku kwadratu.
Pierwiastek z liczby 2 jest tutaj współczynnikiem proporcjonalności prostej.
Ilekroć zmienimy długość boku, to zawsze iloraz długości przekątnej i długości boku będzie taki sam, równy \(\sqrt{2}\).
Jeżeli nie znamy współczynnika proporcjonalności, proporcjonalność prostą możemy wyrazić za pomocą symbolu „~”. Jeżeli napiszemy \(y\) ~ \(x\), to oznacza, że wielkość \(y\) jest wprost proporcjonalna do wielkości \(x\). Wówczas możemy użyć zapisu: \(\frac{y}{x}=const\) i, choć nie wiemy, ile wynosi współczynnik proporcjonalności, to często wystarcza nam wiedza, że jest to wartość niezmienna.
Z wielkościami proporcjonalnymi bardzo często mamy do czynienia w fizyce. Oto taki przykład:
Przykłady
Prawo Ohma mówi, że natężenie prądu stałego I jest proporcjonalne do napięcia elektrycznego U między końcami części obwodu niezawierającej źródeł siły elektromotorycznej. Możemy to zapisać w następujący sposób: I~U. Jest to przykład prawa odkrytego doświadczalnie. Mierząc napięcie U i natężenie prądu I w stałej temperaturze w prostym obwodzie elektrycznym okazuje się, że iloraz \(\frac{U}{I}=const=R\) jest stały. Stałą tę nazwano oporem elektrycznym. Jeżeli zwiększymy napięcie elektryczne w obwodzie elektrycznym, to wiemy, o ile zwiększy się natężenie prądu elektrycznego.
W życiu codziennym bardzo często korzystamy z proporcjonalności prostej. Oto kilka przykładów:
Przykłady
Jacek w ciągu godziny zarobił 3,40 zł. Ile zarobi w ciągu 8 godzin?
Zarobek jest proporcjonalny do czasu pracy. Korzystamy więc z proporcjonalności prostej. Warto ułożyć pewien schemat:
8 h - x zł
1 h - 3,4 zł
Wiemy, że iloraz tych wielkości nie zmienia się, więc: \(\frac{8}{1}=\frac{x}{3,4}\). Najczęściej od razu mnożymy te liczby „na krzyż” i otrzymujemy wynik \(x=3,4\cdot 8=27,2\).
Odpowiedź: Jacek w ciągu 8 godzin zarobi 27,2 zł.
W ciągu jednej godziny piechur przebywa drogę 5 km. Ile czasu zajmie mu przebycie 12 km?
Układamy proporcję:
x h — 12 km
1 h — 5 km
\(\frac{x}{1}=\frac{12}{5}\)
\({x=2,4}\)
Piechur potrzebuje 2,4 godziny na przebycie drogi 12 km. Ile to jest minut? Tutaj również możemy skorzystać z proporcjonalności prostej.
x min - 2,4 h
60 min - 1 h
\(\frac{x}{60}=\frac{2,4}{1}\\{x=144}\)
Odpowiedź: Piechur potrzebuje 144 minut na przebycie drogi 12 km.
Pytania
Co to jest proporcjonalność odwrotna?
Proporcjonalność odwrotna jest szczególnym przypadkiem funkcji homograficznej. O proporcjonalności odwrotnej piszemy tutaj.
Zadania z rozwiązaniami

Zadanie nr 1.
Średnio tygodniowo autor pewnego bloga zarabia na wyświetlaniu reklam na swojej stronie 20 zł. Jakiego zysku może się spodziewać po roku prowadzenia strony?

Zadanie nr 2.
Babcia w ciągu godziny potrafi wydziergać 20 cm szalika. Ile czasu potrwa wydzierganie całego szalika o długości półtora metra?

Zadanie nr 3.
Sekretarka potrafi napisać średnio 50 słów w ciągu jednej minuty na komputerze. Jak długo potrwa ręczne przepisanie książki o objętości 240 stron, jeżeli wiadomo, że średnio jedna strona maszynopisu zawiera 250 słów, a sekretarka jest jednego dnia w stanie pisać bez przerwy przez 5 godzin?

Zadanie nr 4.
Śnieg padał jednostajnie przez 6,5 h. Spadło 19,5 cm śniegu. Ile śniegu spadło w ciągu jednej godziny?

Zadanie nr 5.
Jeden pracownik składa 500 długopisów w ciągu ośmiu godzin pracy. Ilu pracowników trzeba zatrudnić, aby wykonać zlecenie złożenia 10 000 długopisów w ciągu pięciu dni?

Zadanie nr 6.
Wykres ilustruje zależność zaoszczędzonych środków na lokacie od czasu oszczędzania.
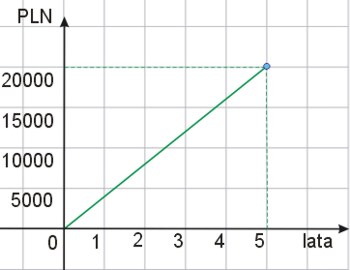
Ile pieniędzy zaoszczędzono po 3 latach oszczędzania?

Zadanie nr 7.
Podczas ostatniego tankowania kierowca wyzerował licznik, przejechał 654 kilometry i zatankował do pełna. Do baku zmieściło się 34,5 l benzyny. Ile litrów na sto kilometrów spala silnik tego samochodu?
Powiązane materiały
© medianauka.pl, 2009-05-30, A-225
Data aktualizacji artykułu: 2023-04-16

 Funkcja liniowa
Funkcja liniowa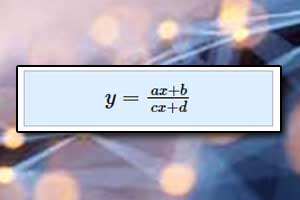 Funkcja homograficzna
Funkcja homograficzna Wykres funkcji liniowej
Wykres funkcji liniowej Funkcja liniowa
Funkcja liniowa



