Funkcja homograficzna

Definicja

Funkcja homograficzna jest to funkcja wymierna w postaci

$y=\frac{ax+b}{cx+d}$

gdzie a, b, c, d są liczbami rzeczywistymi spełniającymi warunek:

$\left|\begin{array}{cc}a&b\\c&d\end{array}\right|=ad-bc\neq{0}$

W przypadku, gdy c=0 funkcja homograficzna staje się funkcją liniową.

Przykład

Oto przykłady funkcji homograficznych:

$y=\frac{2x+1}{x-4}\\y=2x+1\\y=\frac{1}{x}$

Funkcją homograficzną nie jest $y=\frac{4x+4}{2x+2}$ ponieważ ad-bc=0 i ma stałą wartość y=2.

Własności funkcji homograficznej

Z definicji funkcji homograficznej wynika, że dla c różnego od zera

$cx+d\neq{0}\Leftrightarrow{cx}\neq{-d}\Leftrightarrow{x}\neq{-\frac{d}{c}}$ .

Zatem dziedziną funkcji homograficznej jest zbiór R\{-d/c}. W przypadku, gdy c=0 dziedziną funkcji jest cały zbiór liczb rzeczywistych.

Przeciwdziedziną funkcji homograficznej jest zbiór R\{a/c}.

Funkcja homograficzna jest ciągła i różnowartościowa w całej swojej dziedzinie.

Miejsca zerowe funkcji homograficznej

Jeżeli a=0 funkcja homograficzna nie posiada miejsc zerowych. Jeżeli a≠0, to funkcja homograficzna posiada jedno miejsce zerowe x₀=-b/a.

Przykład

Wyznaczmy dziedzinę funkcji $y=\frac{1-x}{x^3-31x+30}$ .

Musimy znaleźć pierwiastki wielomianu znajdującego się w mianowniku. Sprowadza się to do rozwiązania równania algebraicznego Szukamy pierwiastków wśród podzielników wyrazu wolnego: -1, 1, 2, -2, 3, -3, 5, -5, 6, -6, 10, -10, 15, -15. Obliczamy więc wartości wielomianu dla tych liczb.
W(1)=1-31+30=0
W(-1)=-1+31+30=60
W(2)=8-62+30=-24
W(-2)=-8+62+30=84
W(3)=36
W(-3)=96
W(4)=-30
W(-4)=90
W(5)=0
W(-5)=60
W(6)=60
W(-6)=0
Mamy już trzy pierwiastki, więc funkcję możemy zapisać jako $y=\frac{1-x}{(x-5)(x+6)(x-1)}$

Mianownik musi być różny od zera, a zatem wartość zmiennej nie może być równa 1, 5 i -6.

Odpowiedź: Dziedziną funkcji jest zbiór R\{-6,1,5}.

Proporcjonalność odwrotna

Funkcję

$y=\frac{m}{x}$

nazywamy proporcjonalnością odwrotną, a liczbę m nazywamy współczynnikiem proporcjonalności odwrotnej.

W dalszej części lekcji omawiamy wykres funkcji homograficznej.

Inne zagadnienia z tej lekcji

Funkcja wymierna

Funkcja wymierna jest to funkcja w postaci f(x)=A(x)/B(x), gdzie A(x) jest wielomianem zmiennej x, B(x) jest niezerowym wielomianem zmiennej x.

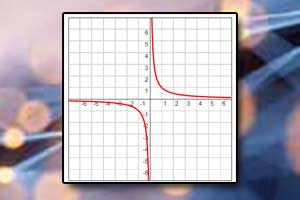Wykres funkcji homograficznej

Wykresem funkcji homograficznej jest hiperbola lub prosta. W tym artykule interesuje nas jedynie hiperbola.

Test wiedzy

Sprawdź swoje umiejętności z materiału zawartego w tej lekcji.