Funkcja wymierna

Funkcja wymierna jest to funkcja w postaci:

\(f(x)=\frac{A(x)}{B(x)}\),

gdzie \(A(x)\) jest wielomianem zmiennej \(x\), \(B(x)\) jest niezerowym wielomianem zmiennej \(x\), którego zbiór wszystkich pierwiastków oznaczymy przez \(\mathbb{P}\). Dziedziną funkcji wymiernej jest \(\mathbb{R}\setminus \mathbb{P}\).

Funkcje wymierne — przykłady

Przykłady funkcji wymiernej:

\(f(x)=\frac{x^3-x^2+4x-1}{x^4-x^3+x^2-1}\)
\(g(x)=\frac{x}{x+1}\)
\(h(x)=\frac{1}{x}\)
\(i(x)=\frac{W(x)}{1}\)

Z ostatniego przykładu wynika, że każdy wielomian jest funkcją wymierną.

Własności funkcji wymiernej

Funkcja wymierna jest ciągła w całej swojej dziedzinie.
Miejscem zerowym funkcji wymiernej jest każdy pierwiastek wielomianu \(A(x)\), który nie jest pierwiastkiem wielomianu \(B(x)\).
Szczególnym przypadkiem funkcji wymiernej jest funkcja homograficzna, która zostanie omówiona w osobnym artykule. W dalszej części lekcji omawiamy także wykres funkcji homograficznej.
Dziedzina funkcji wymiernej — nie jest często wprost do określenia. Aby wyznaczyć dziedzinę funkcji wymiernej, należy znaleźć wszystkie pierwiastki wielomianu \(B(X)\), a następnie wykluczyć je ze zbioru liczb rzeczywistych.
Zbiór wartości funkcji wymiernej, czyli jej przeciwdziedzina nie jest wprost do określenia. Należy zastosować metody analizy funkcji z wykorzystaniem rachunku pochodnych.

Wykres funkcji wymiernej

WYKRESY ONLINE

Narysuj wykres funkcji w programie do szkicowania wykresów i odczytaj jego własności.

Wykres funkcji wymiernej nie jest zwykle łatwo narysować z uwagi na dużą jego zmienność. Na ogół pojawiają się w przebiegu funkcji nieciągłości, różne przedziały monotoniczności, ekstrema lokalne, asymptoty pionowe, poziome i ukośne. Aby narysować wykres funkcji wymiernej, należy na ogół zbadać przebieg zmienności funkcji z wykorzystaniem pojęcia pochodnej funkcji. Szczegółowo temat omawiamy w artykule Badanie przebiegu zmienności funkcji.

Pytania

Czy funkcja \(f(x)=\frac{1}{x}+x\) jest funkcją wymierną?

Zauważmy, że \(\frac{1}{x}+x=\frac{1}{x}+\frac{x^2}{x}=\frac{x^2+1}{x}\). Mamy więc tutaj ogólną postać funkcji wymiernej.

Przykłady

Wyznaczmy dziedzinę funkcji \(y=\frac{1-x}{x^3-31x+30}\).

Musimy znaleźć pierwiastki wielomianu znajdującego się w mianowniku. Sprowadza się to do rozwiązania równania algebraicznego Szukamy pierwiastków wśród podzielników wyrazu wolnego: -1, 1, 2, -2, 3, -3, 5, -5, 6, -6, 10, -10, 15, -15.

Obliczamy więc wartości wielomianu dla tych liczb:

W(1)=1-31+30=0
W(-1)=-1+31+30=60
W(2)=8-62+30=-24
W(-2)=-8+62+30=84
W(3)=36
W(-3)=96
W(4)=-30
W(-4)=90
W(5)=0
W(-5)=60
W(6)=60
W(-6)=0

Mamy już trzy pierwiastki, więc funkcję możemy zapisać jako \(y=\frac{1-x}{(x-5)(x+6)(x-1)}\).

Mianownik musi być różny od zera, a zatem wartość zmiennej nie może być równa 1, 5 i -6.

Odpowiedź: Dziedziną funkcji jest zbiór \(\mathbb{R}\setminus \lbrace -6,1,5\rbrace \).

Zadania z rozwiązaniami

Zadanie nr 1.

Wyznaczyć dziedzinę funkcji \(f(x)=\frac{3x^2-2x+1}{2x^3-3x^2-2x}\).

Pokaż rozwiązanie zadania.

Zadanie nr 2.

Wyznaczyć dziedzinę funkcji \(f(x)=\frac{x^4-x^3+x^2+6x-1}{6x^3-5x^2-2x+1}\)

Pokaż rozwiązanie zadania.

Powiązane materiały

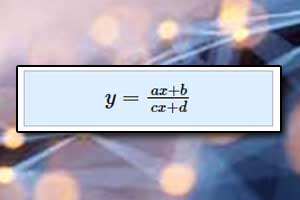Funkcja homograficzna

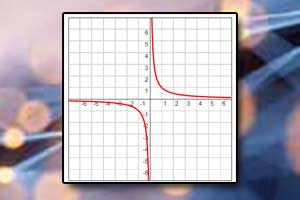Wykres funkcji homograficznej

Funkcja wymierna i homograficzna