Badanie przebiegu zmienności funkcji
Naszkicowanie wykresu funkcji poprzez sporządzenie tabelki zmienności funkcji sprawdza się tylko w przypadku niektórych, prostych funkcji. Zwykle do naszkicowania wykresu funkcji konieczne jest zbadanie przebiegu tej funkcji. Aby zbadać funkcję warto:
- wyznaczyć dziedzinę funkcji,
- znaleźć miejsca zerowe,
- wyznaczyć granice funkcji na krańcach dziedziny funkcji,
- znaleźć asymptoty wykresu funkcji,
- określić monotoniczność funkcji,
- wyznaczyć ekstrema funkcji,
- zbadać parzystość i nieparzystość funkcji.
Wyniki powyższych badań wpisujemy do tabelki i na jej podstawie szkicujemy wykres funkcji.
Badanie zmienności funkcji jest trudne ze względu na szeroki zakres wiedzy, jaki się tutaj wykorzystuje. Wyżej podano linki do artykułów/tematów, których poznanie jest niezbędne przy analizowaniu przebiegu zmienności funkcji.
Najlepiej zobaczyć to na przykładzie:
Przykład
Zbadać przebieg zmienności i narysować szkic wykresu funkcji \(f(x)=\frac{4x}{x+1}+x^2\).
1) Określamy dziedzinę funkcji.
Mamy do czynienia z ułamkiem. Wiemy, że mianownik nie może być równy zero.
\(x+1\neq{0}\)
\(x\neq{-1}\)
\(Df:R\backslash \lbrace -1\rbrace\)
2) Znajdujemy miejsca zerowe funkcji.
\(f(x)=0\)
\(\frac{4x}{x+1}+x^2=0\)
\( \frac{4x}{x+1}+\frac{x^2(x+1)}{x+1}=0\)
\( \frac{4x+x^3+x^2}{x+1}=0\)
Ułamek jest równy zeru, gdy licznik jest równy zeru:
\(4x+x^3+x^2=\)
\(x(x^2+x+4)=0\)
czynnik w nawiasie to trójmian kwadratowy, obliczamy wyróżnik kwadratowy:
\(a=1, b=1, c=4\)
\(\Delta=b^2-4ac=1-16=-15<0\)
Ponieważ wyróżnik trójmianu jest ujemny, więc trójmian nie rozkłada się już na czynniki (nie ma miejsc zerowych). Mamy jedno miejsce zerowe: \(x=0\).
3. Obliczamy granice i wyznaczamy asymptoty.
Zapisaliśmy wyżej, że:
\(f(x)=\frac{4x}{x+1}+x^2=\frac{x^3+x^2+4x}{x+1}\)\
Ułatwi nam to obliczenie niektórych granic. Obliczamy najpierw granicę lewostronną i prawostronną w punkcie \(x=-1\), który nie należy do dziedziny funkcji:
\(\displaystyle\lim_{x\to -1^+}{\frac{x^3+x^2+4x}{x+1}}=[\frac{-4}{0+}]=-\infty\)
\(\displaystyle\lim_{x\to -1^-}{\frac{x^3+x^2+4x}{x+1}}=[\frac{-4}{0-}]=+\infty\)
Mamy więc do czynienia z asymptotą pionową:
\(x=-1\)
Obliczamy granice w plus i minus nieskończoności:
\(\displaystyle\lim_{x\to \pm \infty}{(\frac{4x}{x+1}+x^2)}=+\infty\)
Wykres nie posiada więc asymptoty poziomej.
Szukamy asymptoty ukośnej. W tym celu obliczamy granicę:
\(\displaystyle\lim_{x\to +\infty}{\frac{f(x)}{x}}=\lim_{x\to +\infty}{(\frac{4x}{x^2+x}+x)}=+\infty\)
\(\displaystyle\lim_{x\to -\infty}{\frac{f(x)}{x}}=\lim_{x\to -\infty}{(\frac{4x}{x^2+x}+x)}=-\infty\)
Funkcja nie posiada więc asymptoty pochyłej.
4. Badamy monotoniczność funkcji.
Wykorzystujemy wiedzę na temat zastosowaniu pochodnej funkcji przy wyznaczaniu przedziałów monotoniczności. Obliczamy pochodną funkcji:
\(f'(x)=(\frac{4x}{x+1}+x^2)'=(\frac{4x}{x+1})'+(x^2)'=\frac{4\cdot (x+1)-4x\cdot 1}{(x+1)^2}+2x=\)
\(=\frac{4x+4- 4x}{(x+1)^2}+\frac{2x(x+1)^2}{(x+1)^2} =\frac{4+2x(x^2+2x+1)}{(x+1)^2} =\frac{4+2x^3+4x^2+2x}{(x+1)^2}=\frac{2x^3+4x^2+2x+4}{(x+1)^2}\)
Badamy, kiedy pochodna funkcji jest dodatnia. Mamy do czynienia z ułamkiem o dodatnim mianowniku (jest tam kwadrat liczby). Zatem licznik też musi być dodatni. Mamy więc warunek:
\(2x^3+4x^2+2x+4>0/:2\)
\(x^3+2x^2+x+2>0\)
Rozkładamy wielomian na czynniki. Szukamy pierwiastka wielomianu pośród podzielników wyrazu wolnego: \(-1,1,-2,2\). Ponieważ mamy do czynienia z sumą jednomianów, należy podejrzewać, że pierwiastek jest ujemny:
\(W(-1)=(-1)^3+2\cdot(-1)^2+(-1)+2=-1+2-1+2=2\neq 0\)
\(W(-2)=(-2)^3+2\cdot(-2)^2+(-2)+2=-8+8-2+2=0\)
Liczba \(-2\) jest pierwiastkiem wielomianu, dzielimy go więc przez dwumian \(x-(-2)=x+2\).
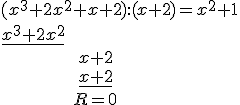
Mamy więc:
\((x+2)(x^2+1)>0\)
Drugi nawias zawiera dwumian, który nie rozkłada się już na czynniki (policz wyróżnik trójmianu kwadratowego).
Czynnik w drugim nawiasie jest zawsze dodatni, więc skoro cały iloczyn ma być dodatni, to czynnik \((x+2)\) też musi być dodatni:
\(x+2>0\)
\(x>-2\)
Zatem dla \(x>-2\) funkcja jest rosnąca.
Przeprowadzając analogiczne rozumowanie, możemy stwierdzić, że funkcja jest malejąca, gdy \(x<-2\).
5. Szukamy ekstremum funkcji.
Funkcja może posiadać maksimum lub minimum w punktach, w których pochodna jest równa zeru. Pochodną wyznaczyliśmy wcześniej:
\(\frac{2x^3+4x^2+2x+4}{(x+1)^2}=0\)
\(2x^3+4x^2+2x+4=0\)
Ostatni krok w rachunkach wynika z tego, iż aby ułamek był równy zero, jego licznik musi być zerem. Mamy do czynienia z wielomianem, który już rozkładaliśmy wcześniej na czynniki:
\((x+2)(x^2+1)=0\)
\(x+2=0\)
\(x=-2\)
Czy w punkcie \(x=-2\) funkcja osiąga ekstremum, a jeśli tak to jakie, przekonamy się po sporządzeniu tabelki zmienności funkcji, gdzie będzie widać, jak pochodna zmienia znak przy przejściu przez ten punkt.
6. Inne cechy funkcji.
Mamy punkt zerowy funkcji, ale warto też znaleźć wartość funkcji w ekstremum (o ile jest):
\(f(-2)=\frac{4\cdot{}(-2)}{-2+1}+(-2)^2=\frac{-8}{-1}+4=12\)
Możemy zbadać parzystość funkcji:
\(f(-x)=\frac{4\cdot{}(-x)}{-x+1}+(-x)^2=\frac{-4x}{-x+1}+x^2\neq f(x)\)
Funkcja nie jest parzysta.
Sprawdzamy nieparzystość funkcji:
\(-f(x)=-\frac{4x}{x+1}-x^2=\neq f(x)\)
Funkcja nie jest nieparzysta.
7. Sporządzamy tabelkę zmienności funkcji.
W pierwszym rzędzie zaznaczamy przedziały zmienności oraz punkty, w których spodziewamy się ekstremum lub takie, które nie należą do dziedziny. W drugim rzędzie zaznaczamy znak pochodnej oraz jej wartość. W trzecim rzędzie za pomocą strzałek zaznaczamy, czy funkcja rośnie czy maleje. Pozwala to wyobrazić sobie przebieg funkcji. Tutaj widać, że funkcja w punkcie \(x=-2\) przechodzi w „dolinę”, ma więc w tym miejscu minimum, (w punkcie \(x=-1\) wykres nie przechodzi w „dolinę” ani „grzbiet”, w tym punkcie funkcja wcale nie jest określona).
| (-∞-2) | -2 | (-2;-1) | -1 | (-1;+∞) | |
|---|---|---|---|---|---|
| \(f'(x)\) | - | 0 | + | + | |
| \(f(x)\) | \(\searrow\) | 12 minimum | \(\nearrow\) | \(\nearrow\) |
Cała trudność w sporządzeniu wykresu polega teraz na zapamiętaniu wszystkich wyników badań funkcji i wykorzystaniu ich przy szkicowaniu. Zobaczmy jak to może wyglądać na podstawie powyższych danych na przykładzie animacji:

Animacja

Zadania z rozwiązaniami

Zadanie nr 1.
Zbadać przebieg zmienności funkcji \(f(x)=x^3+x^2-5x+3\) i naszkicować jej wykres.

Zadanie nr 2.
Zbadać przebieg zmienności funkcji \(f(x)=\frac{x^2-1}{x-4}\) i naszkicować jej wykres.

Zadanie nr 3.
Zbadać przebieg zmienności funkcji \(f(x)=\frac{4x+1}{2x^2-4x}\) i naszkicować jej wykres.

Zadanie nr 4.
Zbadać przebieg zmienności funkcji \(f(x)=\frac{x^3+1}{x^2}\) i naszkicować jej wykres.
Powiązane materiały
© medianauka.pl, 2010-10-03, A-947
Data aktualizacji artykułu: 2024-07-22


 Pochodna funkcji
Pochodna funkcji Równanie stycznej do krzywej
Równanie stycznej do krzywej Pochodna a monotoniczność funkcji
Pochodna a monotoniczność funkcji Pochodna funkcji a ekstremum
Pochodna funkcji a ekstremum Największa i najmniejsza wartość funkcji
Największa i najmniejsza wartość funkcji Test z zastosowania pochodnych
Test z zastosowania pochodnych