Granica funkcji

Będziemy się posługiwać dwoma definicjami pojęcia granicy funkcji. Obie są równoważne. Pojęcie granicy funkcji nie jest łatwe, dlatego warto wcześniej przypomnieć sobie pojęcie granicy ciągu liczbowego. Także obliczanie granic nie jest łatwe. Pomogą w tym wzory, które omawiamy i ilustrujemy przykładami na końcu artykułu. Granice funkcji wykorzystuje się na przykład w analizie przebiegu zmienności funkcji.

Definicja Heinego

Definicja

Funkcja f(x) ma w punkcie x₀ granicę g, jeżeli dla każdego ciągu (x_n) o wyrazach należących do sąsiedztwa punktu x₀ i zbieżnego do x₀ ciąg (f(x_n)) jest zbieżny do g.

Granicę funkcji f(x) w punkcie x₀ będziemy oznaczać następująco: $\lim_{x\to x_0} f(x)=g$ , czytamy przy tym "granicą funkcji f(x) przy x dążącym do x₀ jest g".

Posługujemy się następującym nazewnictwem: (x_n) - ciąg argumentów funkcji, (f(x_n)) - ciąg wartości funkcji. Aby lepiej zrozumieć te pojęcia przeanalizujmy poniższy przykład:

Przykład

Dana jest funkcja y=2x+1.
Weźmy dla przykładu dowolny ciąg: $a_n=\frac{1}{n}$
W prosty sposób możemy utworzyć ciąg argumentów funkcji:
$x_n=\frac{1}{n}$
oraz ciąg wartości funkcji:
$y_n=2x_n+1=2\cdot \frac{1}{n}+1=\frac{2}{n}+1$

Zatem aby obliczyć granicę funkcji w punkcie należy wziąć dowolny ciąg (x_n) zbieżny do x₀ o wyrazach różnych od x₀, a następnie budujemy ciąg wartości funkcji y_n i badamy jego zbieżność.

Animacja

Przykład

Obliczymy granicę funkcji: $y=\frac{1-x}{2}$ w punkcie x₀=2.

Bierzemy dowolny ciąg x_n zbieżny do 2 o wyrazach różnych od 2, czyli $\lim_{n\to\infty}x_n=2,\quad{}x_n\neq{2}$ (takich ciągów jest nieskończenie wiele, nie musimy przy tym znać wzoru na n-ty wyraz ciągu)
Tworzymy ciąg wartości funkcji: $y_n=f(x_n)=\frac{1-x_n}{2}$ i obliczamy jego granicę (zauważ, że obliczamy granicę ciągu, czyli przy n dążącym do nieskończoności!). Granica funkcji f(x) w punkcie 2 będzie więc równa granicy ciągu:
$\lim_{x\to x_0} \frac{1-x}{2}=\lim_{n\to \infty}\frac{1-x_n}{2}=\frac{1-\lim_{n\to \infty}{x_n}}{2}=\frac{1-2}{2}=-\frac{1}{2}$

Nie zawsze funkcja posiada granicę w punkcie. Aby wykazać, że dana funkcja nie ma granicy w punkcie x₀, należy wskazać dwa różne ciągi argumentów zbieżnych do x₀ tak, aby odpowiadające im ciągi wartości funkcji były zbieżne do różnych granic lub aby co najmniej jeden z nich był rozbieżny. Przeanalizujmy to na przykładzie:

Przykład

Obliczymy granicę funkcji: $y=\frac{2x}{x+1}$ w punkcie x₀=-1.

Bierzemy dowolne dwa ciągi x_n zbieżne do -1 o wyrazach różnych od -1:
$x_n=\frac{1}{n}-1$
$x'_n=-\frac{1}{n}-1$

Oba ciągi mają tę samą granicę:

$\lim_{n\to\infty} x_n=\lim_{n\to\infty} x'_n=-1$

Tworzymy ciąg wartości funkcji:
$y_n=f(x_n)=\frac{2(\frac{1}{n}-1)}{1+(\frac{1}{n}-1)}=\frac{\frac{2}{n}-2}{1+\frac{1}{n}-1}=\frac{\frac{2-2n}{n}}{\frac{1}{n}}=\frac{2-2n}{n}\cdot \frac{n}{1}=2-2n$
i obliczamy jego granicę:
$\lim_{x\to -1} \frac{2x}{1+x}=\lim_{n\to \infty}(2-2n)=-\infty$
Tworzymy podobny ciąg wartości funkcji dla drugiego przypadku:
$y'_n=f(x'_n)=\frac{2(-\frac{1}{n}-1)}{1+(-\frac{1}{n}-1)}=\frac{-\frac{2}{n}-2}{1-\frac{1}{n}-1}=\frac{\frac{-2-2n}{n}}{-\frac{1}{n}}=\frac{-2-2n}{n}\cdot \frac{-n}{1}=2+2n$
i obliczamy jego granicę:
$\lim_{x\to -1} \frac{2x}{1+x}=\lim_{n\to \infty}(2+2n)=+\infty$
Otrzymaliśmy dwie różne granice. Nie istnieje więc granica tej funkcji w punkcie -1.

Definicja Cauchy'ego

Definicja

Mówimy, że funkcja f(x) ma w punkcie x₀ granicę g (oznaczamy ją następująco: $\lim_{x\to x_0} f(x)=g$ ), jeżeli dla każdego $\varepsilon >0$ istnieje takie sąsiedztwo S punktu x₀, że dla każdego $x\in$ S spełniona jest nierówność: $|f(x)-g|<\varepsilon$ .

Animacja

Przeanalizujmy przykład. Rozwiążemy zadanie, które rozwiązane zostało przy okazji omawiania definicji Heinego.

Przykład

Wykazać, że $\lim_{x\to 2}\frac{1-x}{2}=-\frac{1}{2}$ .

Obliczamy $f(x)-g=\frac{1-x}{2}-(-\frac{1}{2})=\frac{2-x}{2}$
Nierówność z definicji Cauchy'ego jest spełniona:
$|f(x)-g|<\varepsilon \\ |\frac{2-x}{2}|<\varepsilon \\ -\varepsilon < \frac{2-x}{2}<\varepsilon\\-2\varepsilon < 2-x<2\varepsilon\\-2\varepsilon <x-2<2\varepsilon\\ |x-2|<2\varepsilon$
gdy x należy do sąsiedztwa S(2,2ε).

Wzory

Przy obliczaniu granic w praktyce posługujemy się podstawowymi równościami, które zostały wymienione niżej:

$\lim_{x\to a}{c}=c$

Przykład

$\lim_{x\to 5}{2}=2\\{\lim_{x\to -1}{(-5)}=-5}\\{\lim_{x\to 0}{0}=0}$

$\lim_{x\to a}{x}=a$

Przykład

$\lim_{x\to 5}{x}=5\\ \lim_{x\to -1}{x}=-1\\ \lim_{x\to 0}{x}=0$

$\lim_{x\to a}{\sqrt[n]{x}=\sqrt[n]{a}, \ a> 0, \ n\in N$

Przykład

$\lim_{x\to 5}{\sqrt[3]{x}}=\sqrt[3]{5} \\ \lim_{x\to 9}{\sqrt{x}=\sqrt{9}=3$

$\lim_{x\to a}{\sin{x}}=\sin{a}$

Przykład

$\lim_{x\to 0}{\sin{x}}=\sin{0}=0 \\ \lim_{x\to \frac{\pi}{2}}{\sin{x}}=\sin{\frac{\pi}{2}}=1$

$\lim_{x\to 0}{\frac{\sin{x}}{x}}=1$

Przykład

$\lim_{x\to 0}{\frac{\sin{x}}{x}}=1$

Stosujemy także kilka wzorów rachunku granic. Oto one:

Twierdzenie

Jeżeli funkcja f(x) oraz g(x) mają w punkcie x₀ granice
$\lim_{x\to x_0}{f(x)}=a, \ \lim_{x\to x_0}{g(x)}=b$
to:

$\lim_{x\to x_0}{[f(x)+g(x)]=a+b} \\ \lim_{x\to x_0}{[f(x)-g(x)]=a-b} \\ \lim_{x\to x_0}{[f(x)\cdot g(x)]=a\cdot b} \\ \lim_{x\to x_0}{[f(x):g(x)]=a:b (b\neq 0)}$

Dodatkowo na podstawie powyższych zależności można wywnioskować, że:

$\lim_{x\to x_0}{c\cdot f(x)}=c\cdot \lim_{x\to x_0}{f(x)}$

Oto kilka przykładów obliczania granic funkcji w punkcie z wykorzystaniem powyższych twierdzeń i wzorów:

Przykład

$\lim_{x\to 0}{(x+\sin{x})}=0+\sin{0}=0 \\ \lim_{x\to -1}{(1-x)}=\lim_{x\to -1}{1}-\lim_{x\to -1}{x}=1-(-1)=2 \\ \lim_{x\to \pi}{(x\sin{x})}=\lim_{x\to \pi}{x}\cdot \lim_{x\to \pi}{\sin{x}}=\pi \cdot \sin{\pi}=0\\ \lim_{x\to 1}{\frac{1}{x}}=\frac{\lim_{x\to 1}{1}}{\lim_{x\to 1}{x}}=1$

Zadania z rozwiązaniami

Zadania związane z tematem:
Granica funkcji

Zadanie - granica funkcji w punkcie, definicja Heinego
Oblicz korzystając z definicji Heinego $\lim_{x\to -3}{\frac{x^2-9}{x+3}$

Pokaż rozwiązanie zadania

Zadanie - granica funkcji w punkcie; definicja Heinego
Oblicz korzystając z definicji Heinego $\lim_{x\to 5}{(x+\frac{x-1}{x+1})}$

Pokaż rozwiązanie zadania

Zadanie - granica funkcji, definicja Cauchy'ego
Wykazać na podstawie definicji Cauchy'ego, że $\lim_{x\to -3}{(\frac{x^2-9}{x+3})}=-6$

Pokaż rozwiązanie zadania

Zadanie - granica funkcji na podstawie definicji Cauchy'ego
Wykazać na podstawie definicji Cauchy'ego, że $\lim_{x\to 2}{(5x-7)}=3$

Pokaż rozwiązanie zadania

Zadanie - granica funkcji w punkcie
Wykazać, że funkcja $f(x)=\frac{x^2-|x|}{2x}$ nie ma granicy w punkcie 0.

Pokaż rozwiązanie zadania

Zadanie - granica funkcji
Obliczyć granicę funkcji $\lim_{x\to -1}{\frac{x-5}{1-x^3}}$

Pokaż rozwiązanie zadania

Zadanie - granica funkcji
Obliczyć granicę funkcji $\lim_{x\to 0}{\frac{\sin{3x}}{x}}$

Pokaż rozwiązanie zadania

Zadanie - granica funkcji
Obliczyć granicę funkcji $\lim_{x\to -1}{\frac{x^4-1}{x^2-1}}$

Pokaż rozwiązanie zadania

Zadanie - granica funkcji w punkcie
Obliczyć granicę funkcji $\lim_{x\to 0}{\frac{\sin^2{4x}}{\sin^2{2x}}}$

Pokaż rozwiązanie zadania

Inne zagadnienia z tej lekcji

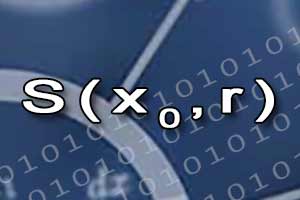Sąsiedztwo punktu
Co to jest sąsiedztwo punktu?

Granica niewłaściwa funkcji
Co to jest granica niewłaściwa funkcji i jak ją obliczamy?

Granica funkcji w nieskończoności
Definicja granicy funkcji w nieskończoności oraz sposoby obliczania granic wielomianów i funkcji wymiernych

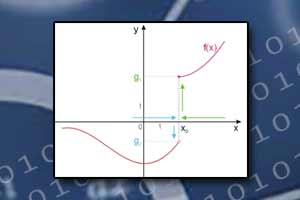Granica lewostronna i prawostronna funkcji
Omówienie granic lewostronnych i prawostronnych funkcji wraz z przykładami

Test wiedzy
Sprawdź swoje umiejętności z materiału zawartego w tej lekcji.

Granica funkcji

Definicja Heinego

Definicja Cauchy'ego

Wzory

Zadania z rozwiązaniami

Inne zagadnienia z tej lekcji

Polecamy w naszym sklepie