Granica niewłaściwa funkcji
Definicja
Niech \(f(x)\) oznacza funkcję, która jest określona w sąsiedztwie \(S\) punktu \(x_0\). Funkcja \(f(x)\) ma w punkcie \(x_0\) granicę niewłaściwą \(\infty\); (używamy zapisu \(\displaystyle \lim_{x\to{x_0}}{f(x)}=\infty\)), jeżeli dla każdego ciągu argumentów \((x_n)\) o wyrazach należących do sąsiedztwa \(S\) zbieżnego do \(x_0\), ciąg wartości \((f(x_n))\) jest rozbieżny do \(\infty\).
Definicja
Niech \(f(x)\) oznacza funkcję, która jest określona w sąsiedztwie \(S\) punktu \(x_0\). Funkcja \(f(x)\) ma w punkcie \(x_0\) granicę niewłaściwą \(-\infty\); (używamy zapisu \(\displaystyle \lim_{x\to{x_0}}{f(x)}=-\infty\)), jeżeli dla każdego ciągu argumentów \((x_n)\) o wyrazach należących do sąsiedztwa \(S\) zbieżnego do \(x_0\), ciąg wartości \((f(x_n))\) jest rozbieżny do \(-\infty\).
Przykład
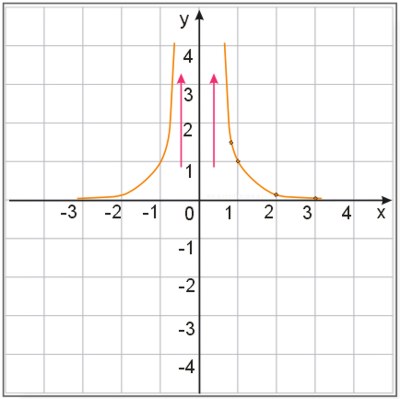
Obliczyć \(\displaystyle \lim_{x\to{0}}{\frac{1}{x^4}}\).
Niech \(x_n\neq{0}, \lim_{n\to\infty}{x_n}=0\).
\(\displaystyle\lim_{x\to{0}}{\frac{1}{x^4}}= \lim_{n\to\infty}{\frac{1}{x_{n}^4}} =\lim_{n\to\infty}{\frac{1}{x_{n}^4}}=\infty\)
Zadania z rozwiązaniami
Inne zagadnienia z tej lekcji
Granica funkcji
Sąsiedztwo punktu
Granica funkcji w nieskończoności
Granica lewostronna i prawostronna funkcji
Granica funkcji© medianauka.pl, 2010-05-05, A-852
Data aktualizacji artykułu: 2023-05-14