Sąsiedztwo punktu

Sąsiedztwem punktu \(x_0\) o promieniu \(r\) nazywamy zbiór \((x_0-r;x_0)\cup(x_0;x_0+r)\).

Sąsiedztwo punktu będziemy oznaczać następująco: \(S(x_0,r)\).

Poniższy rysunek ilustruje pojęcie sąsiedztwa punktu. Jest to zbiór, który na ilustracji został zaznaczony kolorem niebieskim.

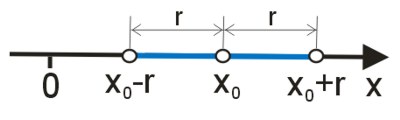
sąsiedztwo punktu

Warto zauważyć podobieństwo między sąsiedztwem punktu a otoczeniem punktu. Do sąsiedztwa punktu \(x_0\) należą wszystkie punkty otoczenia tego punktu z wyjątkiem punktu \(x_0\).

Pytania

Do czego wykorzystuje się pojęcie sąsiedztwa punktu?

Pojęcie to jest wykorzystywanie na przykład przy definiowaniu granicy funkcji, o czym piszemy w dalszej części lekcji.

Jaka jest różnica między sąsiedztwem a otoczeniem punktu?

Wytłumaczymy to na przykładzie zadania. Zadanie brzmi: zaznacz na osi liczbowej otoczenie i sąsiedztwo punktu o współrzędnej 2 o promieniu \(r\). Rozwiązanie ilustruje poniższy rysunek.

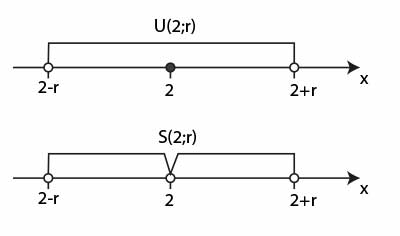
sąsiedztwo a otoczenie punktu

Powiązane materiały

Granica funkcji

Granica niewłaściwa funkcji

Granica funkcji w nieskończoności

Granica lewostronna i prawostronna funkcji

Granica funkcji