Granica lewostronna i prawostronna funkcji
Definicja
Niech \(f(x)\) oznacza funkcję, która jest określona w przedziale \((a;x_0)\). Funkcja \(f(x)\) ma w punkcie \(x_0\) granicę lewostronną \(g\) (używamy zapisu \(\displaystyle\lim_{x\to{x_0-}}{f(x)}=g\)), jeżeli dla każdego ciągu argumentów \((x_n)\) o wyrazach należących do przedziału \((a;x_0)\) zbieżnego do \(x_0\), ciąg wartości \((f(x_n))\) jest zbieżny do \(g\).
Definicja
Niech \(f(x)\) oznacza funkcję, która jest określona w przedziale \((x_0;a)\). Funkcja \(f(x)\) ma w punkcie \(x_0\) granicę prawostronną \(g\) (używamy zapisu \(\displaystyle\lim_{x\to{x_0+}}{f(x)}=g\)), jeżeli dla każdego ciągu argumentów \((x_n)\) o wyrazach należących do przedziału \((x_0;a)\) zbieżnego do \(x_0\), ciąg wartości \((f(x_n))\) jest zbieżny do \(g\).
Twierdzenie
Funkcja \(f(x)\) ma w punkcie \(x_0\) granicę, jeżeli istnieje lewostronna i prawostronna granica funkcji w punkcie \(x_0\) i granice te są równe.
Poniższy rysunek ilustruje różnicę między granicą prawostronną i lewostronną:
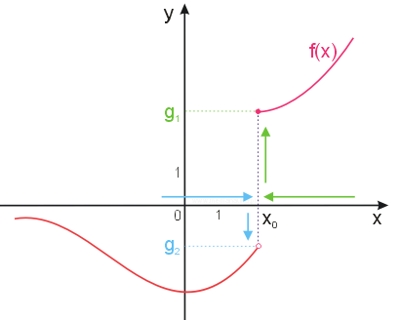
\(\displaystyle\lim_{x\to{x_0-}}{f(x)}=g_2\)
\({\displaystyle\lim_{x\to{x_0+}}{f(x)}=g_1}\)
Funkcja przedstawiona na rysunku ma różną granicą lewostronną i prawostronną, więc w punkcie \(x_0\) nie posiada granicy.
Przykład
Obliczyć granicę lewostronną i prawostronną funkcji \(f(x)=\frac{1}{x}\) w punkcie równym 0.
1) Obliczamy granicę lewostronną:
\(\displaystyle\lim_{x\to{0-}}{\frac{1}{x}}=[\frac{1}{0^-}]=-\infty\)
2) Obliczamy granicę prawostronną:
\(\displaystyle\lim_{x\to{0+}}{\frac{1}{x}}=[\frac{1}{0^+}]=+\infty\)
Wyjaśnienia wymaga zapis w nawiasach kwadratowych. Zapis \(0^-\) w nawiasie kwadratowym oznacza, że \((x)\) jest zbieżne do zera i przyjmuje ujemne wartości. Zapis \(0^+\) w nawiasie kwadratowym oznacza, że \((x)\) jest zbieżne do zera i przyjmuje dodatnie wartości.
Taki zapis ułatwia rachunek granic.
Przyjrzyjmy się granicy prawostronnej. Zgodnie z definicją bierzemy pod uwagę ciąg wartości funkcji \((x_n)\) o wyrazach większych od zera, czyli należących do przedziału \((0;a)\), który jest zbieżny do zera. Granica funkcji prawostronna będzie równa granicy ciągu wartości funkcji \(\lim_{x\to{0+}}{\frac{1}{x}}= \lim_{n\to{\infty}}{\frac{1}{x_n}}\).
Wszystkie wyrazy ciągu argumentów są dodatnie zgodnie z założeniem, ciąg argumentów jest zbieżny do zera, więc ma tu zastosowanie następujące twierdzenie, zgodnie z którym powyższa granica jest równa plus nieskończoności. Zapis z nawiasami kwadratowymi upraszcza całe rozumowanie.
Zadania z rozwiązaniami

Zadanie nr 1.
Obliczyć granicę prawostronną i lewostronną funkcji:
a) \(f(x)=\frac{x+2}{x-1}\) w punkcie \(x_0=2\).
b) \(f(x)=\frac{x-7}{x^2-9}\) w punkcie \(x_0=-3\).

Zadanie nr 2.
Obliczyć granicę prawostronną i lewostronną funkcji:
a) \(f(x)=\frac{x+2}{x-1}\) w punkcie \(x_0=1\).
b) \(f(x)=\frac{2}{x^2}\) w punkcie \(x_0=0\).

Zadanie nr 3.
Obliczyć granicę prawostronną i lewostronną funkcji \(f(x)=\frac{x+|x|}{x}\) w punkcie \(x_0=0\).

Zadanie nr 4.
Obliczyć granicę prawostronną i lewostronną funkcji
\(f(x)=\begin{cases} 5x-x^2+1, \ dla \ x>-1 \\ 5-x, \ dla \ x< -1 \end{cases}\)
w punkcie \(x_0=-1\).
Powiązane materiały
© medianauka.pl, 2010-05-12, A-860
Data aktualizacji artykułu: 2024-07-21

 Sąsiedztwo punktu
Sąsiedztwo punktu Granica funkcji
Granica funkcji Granica niewłaściwa funkcji
Granica niewłaściwa funkcji Granica funkcji w nieskończoności
Granica funkcji w nieskończoności Granica funkcji
Granica funkcji