Obliczanie granic ciągów
Przy obliczaniu granic ciągów korzysta się z wielu właściwości, które zostaną niżej opisane, ale i w oparciu o wiedzę na temat zbieżności elementarnych ciągów. Poniższa tablica zawiera kilka takich ciągów.
Granice ciągów — podstawowe wzory
Poniższa tabela zawiera podstawowe wzory przydatne przy obliczaniu granic ciągów.
| Ciąg | Granica | Przykład |
|---|---|---|
| \(a_n=\frac{1}{n}\) | \(\displaystyle\lim_{n\to\infty} \frac{1}{n}=0\) | - |
| \(a_n=\frac{k}{n}, \quad k\in R\) | \(\displaystyle\lim_{n\to\infty} \frac{k}{n}=0\) | \(\displaystyle\lim_{n\to\infty} \frac{-7}{n}=0\) |
| Ciąg geometryczny: \(a_n=a_1\cdot q^{n-1}, \quad q< 0\) | \(\displaystyle\lim_{n\to\infty} a_1\cdot q^{n-1}=0\) | Dla \(a_1=4\) i \(q=\frac{1}{2}\) otrzymujemy ciąg \((4,2,1,\frac{1}{2},\frac{1}{4},...)\), który jest zbieżny do zera. |
| \(a_n=n^k, \quad k\in N_+\) | \(\displaystyle\lim_{n\to\infty} n^k=\infty\) | \(\displaystyle\lim_{n\to\infty} n^4=\infty\) |
| \(a_n=k^n, \quad k\in N_+\) | \(\displaystyle\lim_{n\to\infty} k^n=\infty\) | \(\displaystyle\lim_{n\to\infty} 4^n=\infty\) |
| Ciąg stały: \(a_n=k, \quad k\in R\) | \(\displaystyle\lim_{n\to\infty} k=k\) | \(\displaystyle\lim_{n\to\infty} 2=2\) |
Twierdzenie o działaniach arytmetycznych na granicach ciągów
Niech \(\displaystyle\lim_{n\to\infty} a_n=a\) oraz \(\displaystyle\lim_{n\to\infty} b_n=b\). Prawdziwe są następujące równości:
\(\displaystyle\lim_{n\to\infty} (a_n+b_n)=a+b\)
\(\displaystyle\lim_{n\to\infty} (a_n-b_n)=a-b\)
\(\displaystyle\lim_{n\to\infty} (a_n\cdot b_n)=a\cdot b\)
\(\displaystyle\lim_{n\to\infty} \frac{a_n}{b_n}=\frac{a}{b},b_n\neq 0,b\neq 0\)
Przykłady
- \(\displaystyle\lim_{n\to\infty} (\frac{5}{n}-2)=\lim_{n\to\infty} 5\cdot \frac{1}{n}-\lim_{n\to\infty}2=5\cdot 0 - 2=-2\)
- \(\displaystyle\lim_{n\to\infty} \frac{1}{n^3}=\lim_{n\to\infty} (\frac{1}{n}\cdot \frac{1}{n}\cdot \frac{1}{n})=0\cdot 0\cdot 0=0\)
Jeżeli choć jeden z ciągów z powyższego twierdzenia jest rozbieżny do nieskończoności, to bez dodatkowej analizy nie można nic jednoznacznie stwierdzić o zbieżności ciągu na podstawie twierdzenia o zbieżności sumy, różnicy, iloczynu i ilorazu ciągów.
Obliczanie typowych granic
Poniższy przykład jest dość często występującym przykładem obliczania granic w zadaniach szkolnych. W takim przypadku dzielimy każdy wyraz licznika i mianownika przez największą potęgę zmiennej n występującej w mianowniku.
Przykład 1
\(\displaystyle\lim_{n\to\infty} \frac{n+1}{n^2-5n+1}=\lim_{n\to\infty} \frac{\frac{n}{n^2}+\frac{1}{n^2}}{\frac{n^2}{n^2}-\frac{5n}{n^2}+\frac{1}{n^2}}=\lim_{n\to\infty} \frac{\frac{1}{n}+\frac{1}{n^2}}{1-\frac{5}{n}+\frac{1}{n^2}}=\)
\(=\frac{\displaystyle\lim_{n\to\infty} (\frac{1}{n}+\frac{1}{n^2})}{\displaystyle\lim_{n\to\infty} (1-\frac{5}{n}+\frac{1}{n^2})}=\frac{\displaystyle\lim_{n\to\infty} \frac{1}{n}+\displaystyle\lim_{n\to\infty}\frac{1}{n^2}}{\displaystyle\lim_{n\to\infty}1-\lim_{n\to\infty}\frac{5}{n}+\displaystyle\lim_{n\to\infty}\frac{1}{n^2}}=\frac{0+0}{1-0+0}=0\)
Przykład 2
\(\displaystyle\lim_{n\to\infty} \frac{3n^2+1}{n^2-n+4}=\lim_{n\to\infty} \frac{\frac{3n^2}{n^2}+\frac{1}{n^2}}{\frac{n^2}{n^2}-\frac{n}{n^2}+\frac{4}{n^2}}=\lim_{n\to\infty} \frac{3+\frac{1}{n^2}}{1-\frac{1}{n}+\frac{4}{n^2}}=\)
\(=\frac{\displaystyle\lim_{n\to\infty} (3+\frac{1}{n^2})}{\displaystyle\lim_{n\to\infty} (1-\frac{1}{n}+\frac{4}{n^2})}=\frac{3+0}{1-0+0}=3\)
Obliczanie granicy ciągu na podstawie definicji
Obliczanie wartości granic ciągów na podstawie definicji zostanie przedstawiona na przykładach.
Przykład 1
Obliczyć granicę ciągu z pierwiastkiem \(a_n=\sqrt{n^2+1}+n\).
Jeżeli od razu nie widzimy zbieżności/rozbieżności ciągu, warto narysować sobie szkic wykresu tego ciągu.
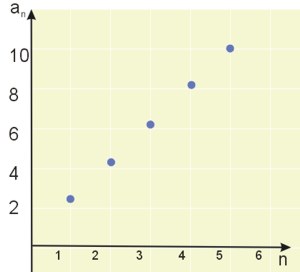
Widzimy, że ciąg jest rozbieżny do nieskończoności. Zgodnie z definicją granicy niewłaściwej ciągu musimy wykazać, że dla każdej liczby rzeczywistej \(M\) prawie wszystkie wyrazy tego ciągu są większe od \(M\).
Zakładamy więc, że \(M\) jest dowolną liczbą rzeczywistą i badamy, dla jakiej wartości \(n_0\) zachodzi \(\sqrt{n^2+1}+n>M\).
Zauważamy, że \(\sqrt{n^2+1}\approx{\sqrt{n^2}=n}\) i:
\(n+n>M\)
\(2n>M/:2\)
\(n>\frac{M}{2}\)
Ponieważ \(n\) jest liczbą naturalną, to przybliżenie wykluczy z prawie wszystkich wyrazów ciągu co najwyżej jeden element, więc możemy powiedzieć, że dla dowolnej liczby rzeczywistej \(M\) począwszy od \(n_0\)-tego wyrazu ciągu (\(n_0>\frac{M}{2}\)) prawie wszystkie wyrazy ciągu są większe od liczby \(M\).
Zgodnie z definicją granicą tego ciągu jest nieskończoność.
\(\displaystyle\lim_{n\to\infty}(\sqrt{n^2+1}+n)=+\infty\)
Przykład 2
Wykazać, że \(\displaystyle\lim_{n\to\infty}\frac{30}{2n+7}=0\).
Zgodnie z definicją granicy ciągu musimy wykazać, że zero jest granicą ciągu \((a_n)\) przy \(n\) dążącym do nieskończoności, jeżeli dla każdego epsilon istnieje taka liczba \(n_0\), że dla każdego \(n>n_0\) spełniona jest nierówność \(|a_n-0|<\varepsilon\), czyli \(|\frac{30}{2n+7}|<\varepsilon\).
Ponieważ wartość wyrażenia pod wartością bezwzględną jest zawsze dodatnia, możemy opuścić wartość bezwzględną i zapisać:
\(\frac{30}{2n+7}<\varepsilon\)
Rozwiązujemy nierówność
\(\frac{30}{2n+7}-\varepsilon<0\)
\(\frac{30-\varepsilon(2n+7)}{2n+7}<0\)
Powyższy ułamek jest mniejszy od zera, jeśli licznik jest ujemny.
\(30-\varepsilon (2n+7)<0\)
\(\varepsilon(2n+7)>30\)
\(2n\varepsilon{>}30-7\varepsilon\)
\(n>\frac{30-7\varepsilon}{2\varepsilon}\)
Istnieje więc takie \(n_0\), równe na przykład \(n_0=[\frac{30-7\varepsilon}{2\varepsilon}]+1\), (zapis [ ] oznacza część całkowitą liczby), że dla każdego numeru wyrazu ciągu większego od\(n_0\) prawie wszystkie wyrazy ciągu spełniają badaną nierówność, więc zero jest granicą tego ciągu.
Twierdzenia o granicach ciągów
Oto wybrane twierdzenia, które dotyczą granic ciągów liczbowych.
Twierdzenie
Prawdziwa jest następująca implikacja:
\(\displaystyle\lim_{n\to\infty}|a_n|=\infty \Rightarrow \lim_{n\to\infty}\frac{1}{a_n}=0\)
Przykład
- \(\displaystyle\lim_{n\to\infty}|2^n|=\lim_{n\to\infty}2^n=\infty \Rightarrow \lim_{n\to\infty}\frac{1}{2^n}=0\)
- \(\displaystyle\lim_{n\to\infty}|n^4|=\lim_{n\to\infty}n^4=\infty \Rightarrow \lim_{n\to\infty}\frac{1}{n^4}=0\)
Twierdzenie
Prawdziwa jest następująca implikacja:
\([(a_n>0)\wedge (\displaystyle\lim_{n\to\infty}a_n=0)] \Rightarrow \lim_{n\to\infty}\frac{1}{a_n}=\infty\)
Przykład
\(\frac{1}{3n+(-1)^n}>0\quad i \quad \displaystyle\lim_{n\to\infty}\frac{1}{3n+(-1)^n}=0\)
\( \Rightarrow \displaystyle\lim_{n\to\infty}[3n+(-1)^n]=+\infty\)
Twierdzenie o trzech ciągach
Poniższe twierdzenie jest wykorzystywanie często tam, gdzie zawodzą inne metody. Stosuje się je na przykład wówczas, gdy we wzorze na n-ty wyraz ciągu pojawia się pierwiastek. Obliczanie granicy ciągu z pierwiastkiem odbywa się więc z wykorzystaniem tego twierdzenia. Oto one:
Twierdzenie o trzech ciągach
Jeżeli dane są ciągi \((a_n), (b_n), (c_n)\), oraz
- \(\displaystyle\lim_{n\to\infty}a_n=\lim_{n\to\infty}c_n=g\)
- istnieje takie \(n_0\in{N_+}\), że dla każdego \(n\geq{n_0}\) prawdziwe są nierówności \(a_n\leq{b_n}\leq{c_n}\),
to ciąg \((b_n)\) jest zbieżny i \(\displaystyle\lim_{n\to\infty}b_n=g\).
Powyższe twierdzenie przeanalizujmy na przykładzie.
Przykład
Wiedząc, że \(\displaystyle\lim_{n\to\infty}\sqrt[n]{c}=1\), gdzie \(c\) jest dowolną liczbą naturalną, obliczymy granicę:
\(\displaystyle\lim_{n\to\infty} \sqrt[n]{5^n+10^n}\)
Możemy zapisać, że:
\(\sqrt[n]{10^n}\leq{\sqrt[n]{5^n+10^n}} \leq{\sqrt[n]{10^n+10^n}}\)
\(10\leq{\sqrt[n]{5^n+10^n}} \leq{10}\sqrt[n]{2}\)
Mamy więc spełniony warunek \(a_n\leq{b_n}\leq{c_n}\).
Pierwszy warunek o równości granic również jest spełniony, gdyż \(\displaystyle\lim_{n\to\infty}10= \lim_{n\to\infty}10\sqrt[n]{2}=10\).
Zatem na podstawie powyższego twierdzenia \(\displaystyle\lim_{n\to\infty}\sqrt[n]{5^n+10^n}=10\).
Zadania z rozwiązaniami

Zadanie nr 1.
Obliczyć granicę \(\displaystyle\lim_{n\to\infty}(\frac{-n^2-4n+1}{n^2+2}-5)\).

Zadanie nr 2.
Obliczyć granicę \(\displaystyle\lim_{n\to\infty}(\frac{n^3+n^2+2n+3}{n+1}-n^2)\).

Zadanie nr 3.
Wykazać, że \(\displaystyle\lim_{n\to\infty}\sqrt{n}=+\infty\).

Zadanie nr 4.
Wykazać na podstawie definicji granicy niewłaściwej, że \(\displaystyle\lim_{n\to\infty}(1+2n)=+\infty\).

Zadanie nr 5.
Wykazać, że \(\displaystyle\lim_{n\to\infty}\frac{1-n^2}{n}=-\infty\).

Zadanie nr 7.
Wykazać na podstawie definicji, że \(\displaystyle\lim_{n\to\infty}\frac{2n+3}{n}=2\).

Zadanie nr 8.
Obliczyć granicę \(\displaystyle\lim_{n\to\infty}\frac{1+2+3+...+n}{n^2+n-1}\).

Zadanie nr 9 — maturalne.
Granica \(\displaystyle\lim_{n\to \infty}{\frac{(pn^2+4n)^3}{5n^6-4}}=-\frac{8}{5}\). Wynika stąd, że
A. \(p=-8\)
B. \(p=4\)
C. \(p=2\)
D. \(p=-2\)

Zadanie nr 10 — maturalne.
Oblicz granicę \(\displaystyle\lim_{n\to \infty}(\frac{11n^3+6n+5}{6n^3+1}-\frac{2n^2+2n+1}{5n^2-4})\). W poniższe kratki wpisz kolejno cyfrę jedności i pierwsze dwie cyfry po przecinku rozwinięcia dziesiętnego otrzymanego wyniku.

Zadanie nr 11 — maturalne.
Ciąg \((a_n)\) jest określony wzorem \(\frac{3n^2+7n-5}{11-5n+5n^2}\) dla każdej liczby naturalnej \(n\geq 1\). Granica tego ciągu jest równa
A. \(3\).
B. \(\frac{1}{5}\).
C. \(\frac{3}{5}\).
D. \(-\frac{5}{11}\).

Zadanie nr 12 — maturalne.
Oblicz granicę
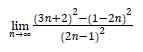 .
.
W poniższe kratki wpisz kolejno – od lewej do prawej – cyfrę jedności i pierwsze dwie cyfry po
przecinku skończonego rozwinięcia dziesiętnego otrzymanego wyniku.


Zadanie nr 13 — maturalne.
Ciąg \((a_n)\) jest określony dla każdej liczby naturalnej \(n\geq 1\) wzorem \(a_n=\frac{(7p-1)n^3+5pn-3}{(p+1)n^3+n^2+p}\), gdzie \(p\) jest liczbą rzeczywistą dodatnią. Oblicz wartość \(p\), dla której granica ciągu \(a_n\) jest równa \(\frac{4}{3}\). W poniższe kratki wpisz kolejno – od lewej do prawej – pierwszą, drugą oraz trzecią cyfrę po przecinku nieskończonego rozwinięcia dziesiętnego otrzymanego wyniku.

Powiązane materiały
© medianauka.pl, 2009-09-05, A-313
Data aktualizacji artykułu: 2023-05-14

 Otoczenie punktu
Otoczenie punktu Granica ciągu
Granica ciągu Granica ciągu
Granica ciągu Ciąg liczbowy
Ciąg liczbowy