Zadanie - obliczanie granicy ciągu
Treść zadania:
Obliczyć granicę \(\displaystyle\lim_{n\to\infty}(\frac{n^3+n^2+2n+3}{n+1}-n^2)\).
Rozwiązanie zadania
Aby obliczyć daną granicę obliczamy najpierw różnicę ciągów, sprowadzając je do wspólnego mianownika:
\(\displaystyle\lim_{n\to\infty}(\frac{n^3+2n^2+2n+3}{n+1}-n^2)=\)\
\(=\displaystyle\lim_{n\to\infty}[\frac{n^3+2n^2+2n+3}{n+1}-\frac{n^2(n+1)}{n+1}]=\)
\( =\displaystyle\lim_{n\to\infty}\frac{n^3+n^2+2n+3-n^2(n+1)}{n+1}=\)
\(=\displaystyle\lim_{n\to\infty}\frac{\cancel{n^3}+\cancel{n^2}+2n+3-\cancel{n^3}-\cancel{n^2})}{n+1}=\)
\(=\displaystyle\lim_{n\to\infty}\frac{2n+3}{n+1}\)
Otrzymaliśmy ciąg w prostej postaci. Aby obliczyć jego granicę, dzielimy licznik i mianownik przez największą potęgę \(n\), występującą w mianowniku. W ten sposób łatwo wyznaczymy granicę tego ciągu.
\(=\displaystyle\lim_{n\to\infty}\frac{\frac{2n}{n}+\frac{3}{n}}{\frac{n}{n}+\frac{1}{n}}=\lim_{n\to\infty}\frac{2+\frac{3}{n}}{1+\frac{1}{n}}=\frac{2+0}{1+0}=2\)
Wyjaśnimy jeszcze poszczególne kroki:
Otóż w przypadku ciągu stałego mamy \(\displaystyle\lim_{n\to\infty}(a)=a\), zatem:
\(\displaystyle\lim_{n\to\infty}2=2\)
\(\displaystyle\lim_{n\to\infty}1=1\)
Korzystając z granicy \(\displaystyle\lim_{n\to\infty}\frac{k}{n}=0, \ k\in \mathbb{R}\) mamy:
\(\displaystyle\lim_{n\to\infty}\frac{3}{n}=0\)
\(\displaystyle\lim_{n\to\infty}\frac{1}{n}=0\)
Odpowiedź
\(\displaystyle\lim_{n\to\infty}(\frac{n^3+n^2+2n+3}{n+1}-n^2)=2\)© medianauka.pl, 2010-01-01, ZAD-479


Zadania podobne
Zadanie nr 1.
Obliczyć granicę \(\displaystyle\lim_{n\to\infty}(\frac{-n^2-4n+1}{n^2+2}-5)\).
Zadanie nr 2.
Wykazać, że \(\displaystyle\lim_{n\to\infty}\sqrt{n}=+\infty\).
Zadanie nr 3.
Wykazać na podstawie definicji granicy niewłaściwej, że \(\displaystyle\lim_{n\to\infty}(1+2n)=+\infty\).
Zadanie nr 4.
Wykazać, że \(\displaystyle\lim_{n\to\infty}\frac{1-n^2}{n}=-\infty\).
Zadanie nr 6.
Wykazać na podstawie definicji, że \(\displaystyle\lim_{n\to\infty}\frac{2n+3}{n}=2\).
Zadanie nr 7.
Obliczyć granicę \(\displaystyle\lim_{n\to\infty}\frac{1+2+3+...+n}{n^2+n-1}\).

Zadanie nr 8 — maturalne.
Granica \(\displaystyle\lim_{n\to \infty}{\frac{(pn^2+4n)^3}{5n^6-4}}=-\frac{8}{5}\). Wynika stąd, że
A. \(p=-8\)
B. \(p=4\)
C. \(p=2\)
D. \(p=-2\)

Zadanie nr 9 — maturalne.
Oblicz granicę \(\displaystyle\lim_{n\to \infty}(\frac{11n^3+6n+5}{6n^3+1}-\frac{2n^2+2n+1}{5n^2-4})\). W poniższe kratki wpisz kolejno cyfrę jedności i pierwsze dwie cyfry po przecinku rozwinięcia dziesiętnego otrzymanego wyniku.

Zadanie nr 10 — maturalne.
Ciąg \((a_n)\) jest określony wzorem \(\frac{3n^2+7n-5}{11-5n+5n^2}\) dla każdej liczby naturalnej \(n\geq 1\). Granica tego ciągu jest równa
A. \(3\).
B. \(\frac{1}{5}\).
C. \(\frac{3}{5}\).
D. \(-\frac{5}{11}\).

Zadanie nr 11 — maturalne.
Oblicz granicę
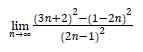 .
.
W poniższe kratki wpisz kolejno – od lewej do prawej – cyfrę jedności i pierwsze dwie cyfry po
przecinku skończonego rozwinięcia dziesiętnego otrzymanego wyniku.


Zadanie nr 12 — maturalne.
Ciąg \((a_n)\) jest określony dla każdej liczby naturalnej \(n\geq 1\) wzorem \(a_n=\frac{(7p-1)n^3+5pn-3}{(p+1)n^3+n^2+p}\), gdzie \(p\) jest liczbą rzeczywistą dodatnią. Oblicz wartość \(p\), dla której granica ciągu \(a_n\) jest równa \(\frac{4}{3}\). W poniższe kratki wpisz kolejno – od lewej do prawej – pierwszą, drugą oraz trzecią cyfrę po przecinku nieskończonego rozwinięcia dziesiętnego otrzymanego wyniku.


