Zadanie - obliczanie granicy niewłaściwej ciągu z definicji
Treść zadania:
Wykazać, że \(\displaystyle\lim_{n\to\infty}\frac{1-n^2}{n}=-\infty\).
Rozwiązanie zadania
Ciąg jest rozbieżny do minus nieskończoności. Zgodnie z definicją granicy niewłaściwej ciągu musimy wykazać, że dla dowolnej liczby rzeczywistej \(M\) prawie wszystkie wyrazy tego ciągu są mniejsze od tej liczby.
Mamy ciąg \(a_n=\frac{1-n^2}{n}\). Wypiszmy kilka pierwszych wyrazów tego ciągu:
\(a_1=\frac{1-1}{1}=0\)
\(a_2=\frac{1-4}{2}=-1\)
\(a_3=\frac{1-9}{3}=-\frac{8}{3}=-2\frac{2}{3}\)
\(a_4=\frac{1-16}{4}=-\frac{14}{4}=-3\frac{3}{4}\)
\(...\)
Zakładamy więc, że \(M\) jest dowolną liczbą rzeczywistą i badamy, dla jakiej wartości \(n_0\):
\(a_n<M\)
\(\frac{1-n^2}{n}<M\)
Otrzymaliśmy nierówność wymierną.
\(\frac{1-n^2}{n}<M\)
\(\frac{1-n^2}{n}-M<0\)
\(\frac{1-n^2}{n}-\frac{Mn}{n}<0\)
\(\frac{1-n^2-Mn}{n}<0\)
Ponieważ \(n\) jest liczbą naturalną, a więc dodatnią, to cały ułamek jest ujemny, gdy licznik jest ujemny. Możemy więc napisać:
\(1-n^2-Mn<0\)
\(-n^2-Mn+1<0/\cdot (-1)\)
\(n^2+Mn-1>0\)
Otrzymaliśmy nierówność kwadratową. Obliczamy więc wyróżnik trójmianu i pierwiastki:
\(a=1,\ b=M,\ c=-1\)
(\Delta=b^2-4ac=M^2+4\)
\(n_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-M-\sqrt{M^2+4}}{2}<0\)
\(n_2=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-M+\sqrt{M^2+4}}{2}\)
Interesują nas tylko dodatnie wartości \(n\) (nie ma ujemnych wyrazów ciągu, tylko \(1,2,3,\) itd.), więc otrzymujemy:
\(n>\frac{-M+\sqrt{M^2+4}}{2}\)
Skąd wiadomo, że \(n_1\) jest ujemne? Wykażemy, że wyrażenie to jest ujemne dla każdej wartości \(M\).
Zauważmy, że \(\sqrt{M^2+4}>\sqrt{M^2}=M\), a także, że:
\(\frac{-M-\sqrt{M^2+4}}{2}<0/\cdot 2\)
\(-M-\sqrt{M^2+4}<0\)
Dla dodatnich wartości \(M\) nierówność jest prawdziwa, natomiast dla ujemnych, pierwszy składnik różnicy staje się liczbą dodatnią. Ponieważ pokazaliśmy wyżej, że \(M\) jest mniejsze od wyrażenia z pierwiastkiem, zatem, gdy od mniejszej liczby odejmiemy większą, otrzymamy liczbę ujemną. Zatem \(n_1\) jest ujemne dla każdej wartości \(M\).
Zatem wykazaliśmy, że dla dowolnej liczby rzeczywistej \(M\) począwszy od \(n_0\)-tego (\(n_0>\frac{-M+\sqrt{M^2+4}}{2}\)) wyrazu ciągu \((a_n)\) prawie wszystkie wyrazy ciągu są mniejsze od liczby \(M\).
Zgodnie z definicją granicą tego ciągu jest minus nieskończoność.
Aby lepiej zrozumieć to rozwiązanie, przeanalizujmy przykład:
Niech np. \(M=-2\). Zgodnie z naszymi wyliczeniami dla \(n_0>\frac{-M+\sqrt{M^2+4}}{2}=\frac{2+\sqrt{8}}{2}= \frac{2+2\sqrt{2}}{2}=1+\sqrt{2}\) prawie wszystkie wyrazy ciągu są mniejsze od \(M\). I rzeczywiście, dopiero dla \(n_0=3,4,5,...\) prawie wszystkie wyrazy ciągu, czyli wszystkie za wyjątkiem wyrazu 1, 2-ego są mniejsze od -2.
© medianauka.pl, 2010-01-02, ZAD-482


Zadania podobne
Zadanie nr 1.
Obliczyć granicę \(\displaystyle\lim_{n\to\infty}(\frac{-n^2-4n+1}{n^2+2}-5)\).
Zadanie nr 2.
Obliczyć granicę \(\displaystyle\lim_{n\to\infty}(\frac{n^3+n^2+2n+3}{n+1}-n^2)\).
Zadanie nr 3.
Wykazać, że \(\displaystyle\lim_{n\to\infty}\sqrt{n}=+\infty\).
Zadanie nr 4.
Wykazać na podstawie definicji granicy niewłaściwej, że \(\displaystyle\lim_{n\to\infty}(1+2n)=+\infty\).
Zadanie nr 6.
Wykazać na podstawie definicji, że \(\displaystyle\lim_{n\to\infty}\frac{2n+3}{n}=2\).
Zadanie nr 7.
Obliczyć granicę \(\displaystyle\lim_{n\to\infty}\frac{1+2+3+...+n}{n^2+n-1}\).

Zadanie nr 8 — maturalne.
Granica \(\displaystyle\lim_{n\to \infty}{\frac{(pn^2+4n)^3}{5n^6-4}}=-\frac{8}{5}\). Wynika stąd, że
A. \(p=-8\)
B. \(p=4\)
C. \(p=2\)
D. \(p=-2\)

Zadanie nr 9 — maturalne.
Oblicz granicę \(\displaystyle\lim_{n\to \infty}(\frac{11n^3+6n+5}{6n^3+1}-\frac{2n^2+2n+1}{5n^2-4})\). W poniższe kratki wpisz kolejno cyfrę jedności i pierwsze dwie cyfry po przecinku rozwinięcia dziesiętnego otrzymanego wyniku.

Zadanie nr 10 — maturalne.
Ciąg \((a_n)\) jest określony wzorem \(\frac{3n^2+7n-5}{11-5n+5n^2}\) dla każdej liczby naturalnej \(n\geq 1\). Granica tego ciągu jest równa
A. \(3\).
B. \(\frac{1}{5}\).
C. \(\frac{3}{5}\).
D. \(-\frac{5}{11}\).

Zadanie nr 11 — maturalne.
Oblicz granicę
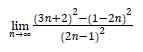 .
.
W poniższe kratki wpisz kolejno – od lewej do prawej – cyfrę jedności i pierwsze dwie cyfry po
przecinku skończonego rozwinięcia dziesiętnego otrzymanego wyniku.


Zadanie nr 12 — maturalne.
Ciąg \((a_n)\) jest określony dla każdej liczby naturalnej \(n\geq 1\) wzorem \(a_n=\frac{(7p-1)n^3+5pn-3}{(p+1)n^3+n^2+p}\), gdzie \(p\) jest liczbą rzeczywistą dodatnią. Oblicz wartość \(p\), dla której granica ciągu \(a_n\) jest równa \(\frac{4}{3}\). W poniższe kratki wpisz kolejno – od lewej do prawej – pierwszą, drugą oraz trzecią cyfrę po przecinku nieskończonego rozwinięcia dziesiętnego otrzymanego wyniku.


