Granica ciągu

Definicja granicy ciągu wymaga zrozumienia pojęcia otoczenia punktu oraz wygodnie jest posłużyć się pojęciem „prawie wszystkich wyrazów ciągu nieskończonego”.

Prawie wszystkie wyrazy ciągu to wszystkie wyrazy ciągu z wyjątkiem co najwyżej skończonej ich liczby.

Przykłady

Dany jest ciąg \((1,2,3,4,5,...)\).

Wszystkie wyrazy ciągu większe od \(100\), to prawie wszystkie wyrazy tego ciągu.
Wszystkie wyrazy ciągu z wyjątkiem liczb \(10,11,12,13,...,100000\) to prawie wszystkie wyrazy ciągu.

Przykładami prawie wszystkich wyrazów ciągu nie są:

wszystkie wyrazy ciągu mniejsze od \(100\)
wszystkie wyrazy ciągu z wyjątkiem liczb \(2,4,6,8,...\)

ponieważ wykluczamy z ciągu nieskończoną liczbę wyrazów.

Zrozumienie definicji granicy ciągu jest trudne, chociaż intuicyjne podejście często jest oczywiste. Dlatego zaczniemy od przykładu.

Przykłady

Dany jest ciąg \(a_n=\frac{2+n}{n}\).

Wypiszmy jego wyrazy i sporządźmy wykres tego ciągu.

\((3, 2, 1\frac{2}{3}, 1\frac{1}{2}, 1\frac{2}{5}, 1\frac{1}{3}, 1\frac{2}{7}, 1\frac{1}{4}, 1\frac{2}{9}, 1\frac{1}{5}, ...)\)

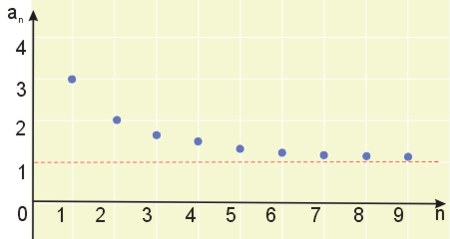
Wykres ciągu an=(2+n)/n

Bez trudu zauważamy, że im większe \(n\), tym wyrazy \(a_n\) są bliższe wartości \(1\). Mówimy, że ciąg jest zbieżny do \(1\) lub że jego granicą przy \(n\) dążącym do nieskończoności jest liczba \(1\). Możemy też powiedzieć, że \(a_n\) dąży do \(1\), gdy \(n\) dąży do nieskończoności.

Definicja granicy ciągu

Zajmijmy się teraz definicją granicy ciągu. Oto ona:

Liczba \(g\) jest granicą ciągu \((a_n)\) (granicę oznaczamy symbolem \(\displaystyle\lim_{n\to\infty} (a_n)=g\)), jeżeli spełniony jest warunek:

\(\displaystyle\lim_{n\to\infty} (a_n)=g \Leftrightarrow \bigwedge\limits_{\varepsilon >0} \bigvee\limits_{n_0} \bigwedge\limits_{n >n_0}|a_n-g|<\varepsilon\)

Powyższy wzór możemy przeczytać następująco: „Liczba \(g\) jest granicą ciągu \((a_n)\) przy \(n\) dążącym do nieskończoności, jeżeli dla każdego \(\varepsilon\) istnieje taka liczba \(n_0\), że dla każdego \(n>n_0\) spełniona jest nierówność \(|a_n-g|<\varepsilon\)”.

Symbol lim czytamy jako limes. Jest słowo greckiego pochodzenia, oznaczające granicę.

Symbol \(\displaystyle\lim_{n\to\infty}(a_n)=g\) czytamy następująco: „granicą ciągu \(a_n\) przy \(n\) dążącym do nieskończoności, jest liczba \(g\)”.

Jeśli przypomnimy sobie pojęcia otoczenia punktu i prawie wszystkich wyrazów ciągu, to powyższa definicja powinna się wydawać bardziej zrozumiała.
Otóż widać, że \(\varepsilon\) to promień otoczenia punktu \(g\), a wyrazy ciągu \(a_n\) należą do tego otoczenia.

Możemy więc powiedzieć, że liczba \(g\) jest granicą ciągu, jeżeli dla dowolnego otoczenia punktu g prawie wszystkie wyrazy tego ciągu (wszystkie dla \(n\) większego od \(n_0\)) należą do tego otoczenia.

Jeszcze lepiej widać to na ilustracji.

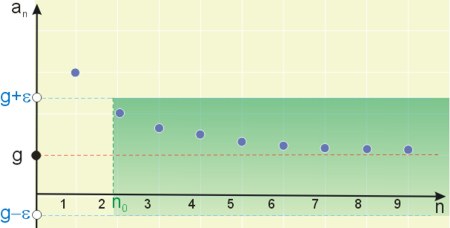
granica coągu

Zaznaczyliśmy na wykresie przykładowe otoczenie punktu \(g=1\) i widać, że istnieje takie \(n_0\), że dla kolejnych \(n\) większych od \(n_0\) prawie wszystkie wyrazy \(a_n\) należą do otoczenia tego punktu — punkty \((n, a_n)\) znajdują się do zakreskowanej części wykresu. Widać też, że dotyczy to każdego otoczenia tego punktu. Stąd możemy napisać, że:

\(\displaystyle\lim_{n\to\infty}\frac{n+2}{n}=1\)

Granica niewłaściwa ciągu

Nie wszystkie granice ciągów są zbieżne. Spójrzmy na poniższe przykłady.

Przykłady

Ciąg \((2,4,8,...,2^n,...)\) nie jest zbieżny.
Ciąg \((1,4,9,16,...,n^2,...)\) również nie jest zbieżny.

O ciągach, które nie mają granicy, mówimy, że są rozbieżne lub mają granice niewłaściwe.

Definicja

Ciąg \((a_n)\) nazywamy rozbieżnym do nieskończoności i piszemy \(\displaystyle\lim_{n\to\infty}(a_n)=\infty\), jeżeli:

\(\displaystyle\lim_{n\to\infty}(a_n)=\infty\Leftrightarrow\bigwedge\limits_{M\in{R}}\bigvee\limits_{n_0\in{N_{+}}}\bigwedge\limits_{n\in{N_{+}}}(n>n_0\Rightarrow{a_n>M})\)

Powyższą definicję możemy przeczytać następująco: „Ciąg \((a_n)\) nazywamy rozbieżnym do nieskończoności (ma granicę niewłaściwą nieskończoność), jeżeli dla każdej liczby rzeczywistej \(M\) prawie wszystkie wyrazy tego ciągu są większe od \(M\)”.

Definicja

Ciąg \((a_n)\) nazywamy rozbieżnym do minus nieskończoności i piszemy \(\displaystyle\lim_{n\to\infty}(a_n)=-\infty\), jeżeli

\(\displaystyle\lim_{n\to\infty}(a_n)=-\infty\Leftrightarrow\bigwedge\limits_{M\in{R}}\bigvee\limits_{n_0\in{N_{+}}}\bigwedge\limits_{n\in{N_{+}}}(n>n_0\Rightarrow{a_n}<M)\)

Powyższą definicję możemy przeczytać następująco: „Ciąg \((a_n)\) nazywamy rozbieżnym do minus nieskończoności (ma granicę niewłaściwą minus nieskończoność), jeżeli dla każdej liczby rzeczywistej \(M\) prawie wszystkie wyrazy tego ciągu są mniejsze od \(M\)”.

Przykłady ciągów rozbieżnych i ich granice:

Ciąg \((a_n>)\)	Granica
\(a_n=n\)	\(\displaystyle\lim_{n\to\infty}n=\infty\)
\(a_n=-n\)	\(\displaystyle\lim_{n\to\infty}(-n)=-\infty\)
\(a_n=5^n\)	\(\displaystyle\lim_{n\to\infty}5^n=\infty\)
\(a_n=n^3\)	\(\displaystyle\lim_{n\to\infty}n^3=\infty\)

Inne zagadnienia z tej lekcji

Otoczenie punktu

Obliczanie granic ciągów

Granica ciągu