Funkcja
Funkcję zapisujemy w następujący sposób:
\(f(x)=x \rightarrow y\), gdzie \( x \in X, y \in Y\)
lub prościej:
\(y=f(x)\), gdzie \( x \in X, y \in Y\)
Argument i wartość funkcji
Element \(x\) nazywamy argumentem funkcji lub zmienną niezależną.
Element \(y\) nazywamy wartością funkcji lub zmienną zależną.
Przykłady
Dziedzina i przeciwdziedzina funkcji
Zbiór \(X\) nazywamy dziedziną funkcji i często oznaczamy przez \(D_{f}\).
Używamy także pojęcia przeciwdziedziny (zbioru wartości funkcji). Jest to zbiór takich \(y \in Y\), dla których istnieje \(x \in X\) takie, że \(y=f(x)\). Przeciwdziedzinę oznaczamy przez \(D_{f}^{-1}\).
W praktyce warunek \(y \in Y\) pomijamy, natomiast pomijając warunek \(x \in X\) przyjmujemy, że dziedziną funkcji jest zbiór wszystkich liczb, dla których spełniona jest prawa strona równości \(y=f(x)\).
Jeżeli mamy do czynienia z przypadkiem, w którym każdy element zbioru \(Y\) jest przyporządkowany co najmniej jednemu elementowi ze zbioru \(X\), to mówimy, że zbiór \(X\) jest odwzorowany na zbiór \(Y\). W takim przypadku zbiór \(Y\) jest przeciwdziedziną funkcji.
Przykłady
Przykład 1
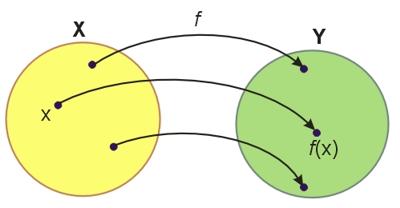
Rysunek ilustruje przykład funkcji \(f\), która każdemu elementowi \(x\) ze zbioru \(X\) przyporządkowuje dokładnie jeden element ze zbioru \(Y\). Dziedzina jest tutaj trójelementowa, przeciwdziedzina również ma trzy elementy. Przykład ten ilustruje odwzorowanie zbioru \(X\) na zbiór \(Y\). W takim odwzorowaniu przeciwdziedziną jest cały zbiór \(Y\).
Określaniem dziedziny i przeciwdziedziny funkcji zajmiemy się w kolejnych artykułach (linki na dole).
Przykład 2
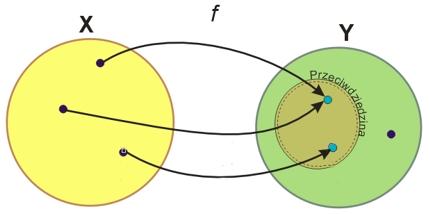
Tutaj również mamy do czynienia z funkcją, mimo że w zbiorze \(Y\) znajduje się element nieprzyporządkowany żadnemu elementowi ze zbioru \(X\). Mamy więc do czynienia z odwzorowaniem zbioru \(X\) w zbiór \(Y\) (nie jest to odwzorowanie „na”) i w tym przypadku zbiór \(Y\) nie jest przeciwdziedziną funkcji. Przeciwdziedzina, zaznaczona w zbiorze \(Y\) innym kolorem, jest jego podzbiorem. Warto zauważyć, że dwa elementy ze zbioru \(X\) są przypisane do tego samego elementu ze zbioru \(Y\).
Przykład 3
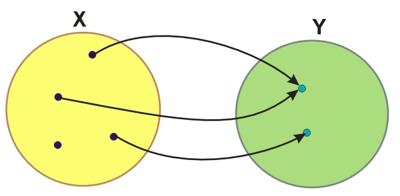
Przyporządkowanie, które zostało zilustrowane na powyższym rysunku, nie jest funkcją, gdyż nie każdemu elementowi ze zbioru \(X\) przyporządkowano element ze zbioru \(Y\) (w zbiorze \(X\) pozostał 1 element, który nie jest przyporządkowany).
Przykład 4
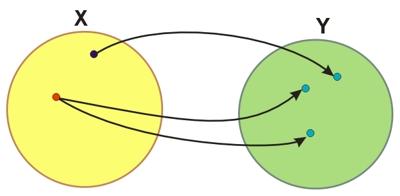
Przyporządkowanie, które zostało zilustrowane na powyższym rysunku, nie jest funkcją, gdyż jednemu elementowi ze zbioru \(X\) (zaznaczono go na czerwono) przyporządkowano aż dwa elementy ze zbioru \(Y\), a w myśl definicji funkcji, ma być przyporządkowany dokładnie jeden element.
Przykłady funkcji
A oto inne przykłady funkcji:
Każdemu z 25 uczniów klasy I przyporządkowano numer w dzienniku.
Jest to przykład funkcji. Dziedziną jest tutaj 25-elementowy zbiór uczniów, przeciwdziedziną zbiór liczb naturalnych z zakresu od 1 do 25. Jest to ponadto odwzorowanie zbioru \(X\) na zbiór \(Y\).
Każdej liczbie rzeczywistej przyporządkowujemy liczbę o jeden większą.
Jest to przykład funkcji liczbowej. Możemy ją zapisać w postaci: \(y=x+1\). Dziedziną i przeciwdziedziną jest tutaj zbiór liczb rzeczywistych \(\mathbb{R}\).
Każdej liczbie rzeczywistej przyporządkowujemy jej kwadrat.
Jest to przykład funkcji liczbowej. Możemy ją zapisać w postaci: \(f(x)=x^2\). Dziedziną i przeciwdziedziną jest tutaj zbiór liczb rzeczywistych \(\mathbb{R}\).
Każdej liczbie rzeczywistej przyporządkowujemy liczbę 1.
Jest to przykład funkcji liczbowej. Możemy ją zapisać w postaci: \(f(x)=1\). Dziedziną jest tutaj zbiór liczb rzeczywistych \(\mathbb{R}\), natomiast przeciwdziedziną zbiór {1}.
Każdej liczbie rzeczywistej przyporządkowujemy jej odwrotność.
Jest to przykład funkcji liczbowej. Możemy ją zapisać w postaci: \(y=\frac{1}{x}\). Dziedziną i przeciwdziedziną jest tutaj zbiór \(\mathbb{R}\setminus \lbrace0 \rbrace\).
Każdemu trójkątowi przyporządkowujemy jego pole powierzchni.
Jest to przykład funkcji. Dziedziną jest zbiór wszystkich trójkątów. Przeciwdziedziną jest tutaj zbiór \(\mathbb{R}_+\).
Własności funkcji, rodzaje funkcji oraz ich wykresy są omawiane w kolejnych artykułach o funkcjach.
Zadania z rozwiązaniami

Zadanie nr 1 — maturalne.
W kartezjańskim układzie współrzędnych \((x,y)\) narysowano wykres funkcji \(y=f(x)\) (zobacz rysunek).
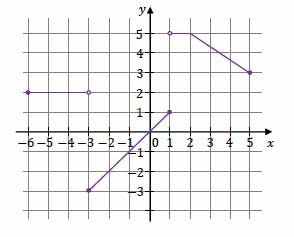
1. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Dziedziną funkcji \(f\) jest zbiór
A. \([−6,5]\)
B. \((−6,5)\)
C. \((−3,5]\)
D. \([−3,5]\)
2. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Największa wartość funkcji \(f\) w przedziale \([−4,1]\) jest równa
A. \(0\)
B. \(1\)
C. \(2\)
D. \(5\)
3. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Funkcja \(f\) jest malejąca w zbiorze
A. \([−6,−3)\)
B. \([−3,1]\)
C. \((1,2]\)
D. \([2,5]\)

Zadanie nr 2 — maturalne.
Właściciel pewnej apteki przeanalizował dane dotyczące liczby obsługiwanych klientów z 30 kolejnych dni. Przyjmijmy, że liczbę \(L\) obsługiwanych klientów \(n\)-tego dnia opisuje funkcja \(L(n)=-n^2+22n+279\), gdzie \(n\) jest liczbą naturalną spełniającą warunki \(n\geq 1\) i \(n\leq 30\).
Oceń prawdziwość poniższych stwierdzeń. Wybierz \(P\), jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe.
| Łączna liczba klientów obsłużonych w czasie wszystkich analizowanych dni jest równa \(L(30)\). | P | F |
| W trzecim dniu analizowanego okresu obsłużono 336 klientów. | P | F |
Którego dnia analizowanego okresu w aptece obsłużono największą liczbę klientów? Oblicz liczbę klientów obsłużonych tego dnia. Zapisz obliczenia.
Powiązane materiały
 Funkcja
Funkcja Funkcja — quiz
Funkcja — quiz© medianauka.pl, 2009-04-28, A-190
Data aktualizacji artykułu: 2023-03-31

 Wartości i argumenty funkcji
Wartości i argumenty funkcji Wyznaczanie dziedziny funkcji
Wyznaczanie dziedziny funkcji Funkcja — podstawowe pojęcia
Funkcja — podstawowe pojęcia Wykres funkcji
Wykres funkcji Miejsce zerowe funkcji
Miejsce zerowe funkcji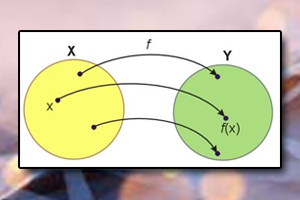 Funkcja różnowartościowa
Funkcja różnowartościowa Funkcja odwrotna i tożsamościowa
Funkcja odwrotna i tożsamościowa Funkcja złożona
Funkcja złożona Dziedzina funkcji — quiz
Dziedzina funkcji — quiz Wartości i argumenty funkcji — quiz
Wartości i argumenty funkcji — quiz Miejsca zerowe — quiz
Miejsca zerowe — quiz