Funkcja odwrotna i funkcja tożsamościowa

Zajmiemy się w niniejszym artykule dwoma pojęciami związanymi z podstawowymi właściwościami funkcji.

Funkcja odwrotna

Jeżeli różnym elementom \(x\) ze zbioru \(X\) są przyporządkowane różne elementy \(y\) ze zbioru \(Y\) za pomocą funkcji \(f\), to możemy również każdemu elementowi \(y\) ze zbioru \(Y\) przyporządkować dokładnie jeden element \(x\) ze zbioru \(X\) tak, że obrazem \(x\) w odwzorowaniu \(f\) jest \(y\).
W ten sposób stworzyliśmy funkcję odwrotną do funkcji \(f\) i oznaczamy ją przez \(f^{-1}\).

Warunek konieczny i wystarczający na to, aby funkcja \(f:X\rightarrow Y\) posiadała funkcję odwrotną, jest następujący: funkcja f musi być różnowartościowa, a zbiór \(Y\) zbiorem wartości funkcji \(f\).

Odwzorowanie, do którego istnieje odwzorowanie odwrotne, nazywamy wzajemnie jednoznacznym albo odwracalnym.

Oczywiście nie każda funkcja posiada funkcję odwrotną. Na przykład funkcja \(f(x)=5\) nie posiada funkcji odwrotnej, gdyż nie jest to funkcja różnowartościowa.

Aby znaleźć funkcję odwrotną do funkcji \(y=f(x)\), wystarczy wyrazić \(x\) poprzez wartość \(y\) i w ten sposób otrzymujemy funkcję \(x=g(y)\). Zamieniając ze sobą symbole \(x\) i \(y\) otrzymujemy wzór funkcji odwrotnej.

Przykłady funkcji odwrotnych

Znajdziemy funkcję odwrotną do \(y=2x+1\).

Wyznaczamy \(x\) z powyższego równania:

\(2x=y-1\)

\(x=\frac{1}{2}y-\frac{1}{2}\)

Zamieniamy teraz ze sobą symbole \(x\) i \(y\) i otrzymujemy wzór funkcji odwrotnej: \(y=\frac{1}{2}x-\frac{1}{2}\).

Funkcja tożsamościowa

Odwzorowaniem tożsamościowym nazywamy odwzorowanie zbioru \(X\) na \(X\), takie że \(x\rightarrow y=x\).

Przykład funkcji tożsamościowej

Przykładem funkcji tożsamościowej jest funkcja \(f(x)=x\). Funkcja \(f(x)=2x\) już tożsamościowa nie jest.

Ćwiczenia

Zwiększ populację dziobaków, rozwiązując krótkie zadania i ćwiczenia związane z tą lekcją.

Nie jesteś zalogowany.

Z jajka nic się nie wykluje, a Twoja populacja dziobaków nie przetrwa po opuszczeniu strony... Zaloguj się

Aby otworzyć złote jaja, musisz posiadać Plan Premium.

Zadania z rozwiązaniami

Zadanie nr 1.

Znaleźć funkcję odwrotną do funkcji \(y=2x-5\).

Pokaż rozwiązanie zadania.

Powiązane materiały

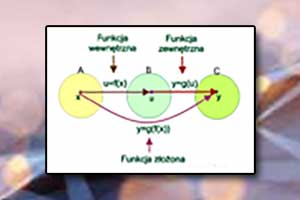Funkcja złożona

Funkcja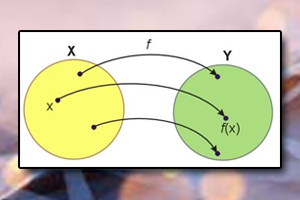

Funkcja różnowartościowa

Funkcja odwrotna i funkcja złożona