Implikacja

Co to jest implikacja?

Implikacja (wynikanie) jest to zdanie „jeżeli p, to q” i zapisujemy: p ⇒ q.

Zdanie p nazywamy poprzednikiem, a zdanie q następnikiem, a znak ⇒ czytamy „implikuje” lub „z ... wynika ...”

Wynikanie logiczne — przykłady

Przykłady implikacji:

Jeżeli liczba naturalna jest podzielna przez 9, to liczba ta jest podzielna przez 3.
Jeżeli figura geometryczna posiada 3 boki, to figura jest kwadratem.
Jeżeli reszta z dzielenia liczby N jest równa 0, to liczba N jest parzysta.

Wyznaczenie wartości logicznej implikacji nie jest tak proste, jak w przypadku koniunkcji, czy alternatywy, ponieważ w języku potocznym wynikanie stosuje się w węższym zakresie.

Poniższa tabela zawiera wartości logiczne zdań i ich implikacji:

p	q	p ⇒ q
0	0	1
0	1	1
1	0	0
1	1	1

Jak widać w tabeli, implikacja jest fałszywa tylko w przypadku, gdy z prawdy wynika fałsz. Innymi słowy, z prawdy wynika tylko prawda Warto też zauważyć, że z fałszu może wynikać prawda (wiersz 2 tabeli)!

Przykłady

Przeanalizujmy wartości logiczne implikacji na przykładach:

Dla N = 7 zdanie p: „liczba naturalna N jest podzielna przez 9” jest fałszywe i zdanie q: „liczba N jest podzielna przez 3” jest fałszywe, a implikacja „jeżeli liczba naturalna N jest podzielna przez 9, to liczba N jest podzielna przez 3” przyjmuje wartość logiczną 1 — jest prawdziwa (wiersz 1).
Dla N = 3 zdanie p jest fałszywe (3 nie jest podzielne przez 9), ale zdanie q jest prawdziwe (3 jest podzielne przez 3), natomiast implikacja jest prawdziwa (wiersz 2).
Nie ma takiej liczby, która będąc podzielną przez 9, nie byłaby podzielna przez 3 (wiersz 3). Natomiast rozpatrzmy przykład z figurą geometryczną f. Niech f będzie trójkątem. Zdanie m: „figura geometryczna f posiada 3 boki” jest prawdziwe, natomiast zdanie n: „figura f jest kwadratem” jest oczywiście fałszywe. Zatem implikacja „jeżeli figura geometryczna f posiada 3 boki, to figura f jest kwadratem” jest fałszywa.
Dla N = 18 zdanie p jest prawdziwe (18 jest podzielne przez 9) i zdanie q jest prawdziwe (18 jest podzielne przez 3) i implikacja przyjmuje wartość logiczną 1 (wiersz 4).

Poniżej przedstawione zostały podstawowe prawa logiki, stanowiące podstawę wszystkich dowodów matematycznych.

Reguła odrywania

Jeżeli prawdziwe są implikacja p ⇒ q i zdanie p, to zdanie q jest prawdziwe.

Reguła przechodniości implikacji

Jeżeli prawdziwe są implikacje: p ⇒ q oraz q ⇒ r, to prawdziwa jest implikacja p ⇒ r.

Zaprzeczenie implikacji

Negacja implikacji to następująca tautologia:

(~ (p ⇒ q) ) ⇔ ( p ∧ (~ q))

Zaprzeczenie implikacji ~ (p ⇒ q) jest równoważne koniunkcji p ∧ (~ q).

Warunek konieczny i wystarczający

Jeżeli ze zdania p wnika zdanie q, to p jest warunkiem wystarczającym (dostatecznym) dla q, a q jest warunkiem koniecznym dla q.

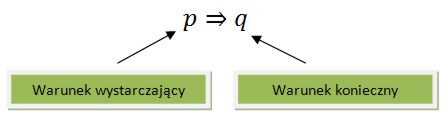
Przykłady

Niech p oznacza zdanie: liczba N jest podzielna przez 10.
Niech q oznacza zdanie: liczba N jest podzielna przez 5.

Zdanie p jest warunkiem wystarczającym dla q (podzielność liczby przez 10 jest warunkiem wystarczającym podzielności liczby przez 5).

Zdanie q jest warunkiem koniecznym dla p (podzielność liczby przez 5 jest warunkiem koniecznym podzielności przez 10).

Ciekawe jest to, że zdanie q (podzielność przez 5) nie jest warunkiem wystarczającym dla p — podzielności przez 10 (na przykład dla N = 15), a także p nie jest warunkiem koniecznym dla q (na przykład liczba 5 jest podzielna przez 5, ale nie dzieli się przez 10).

Jeżeli warunek konieczny jest jednocześnie warunkiem wystarczającym, to mówimy wówczas, że jest to warunek konieczny i wystarczający.

Jeżeli rozbudujemy nieco powyższy przykład w taki sposób, że zdanie q będzie zdefiniowane jako: liczba N jest parzysta i podzielna przez 5, to otrzymamy przykład warunku koniecznego i wystarczającego, a mianowicie: podzielność liczby parzystej N przez 5 jest warunkiem koniecznym i wystarczającym dla podzielności liczby przez 10.

Pytania

Co to jest następnik i poprzednik?

W logice poprzednik jest pierwszym członem implikacji.

Następnik jest drugim członem implikacji.

Ćwiczenia

Ćwiczenia interakcyjne pomogą przygotować się na sprawdzian, test, egzamin, a ponadto usystematyzują wiedzę z danej dziedziny. To także świetny trening do matury. Wiele ćwiczeń to dobre zadania maturalne.

ĆWICZENIA

Implikacja

Powiązane quizy

Logika — quiz

Liczba pytań: 22
Quiz szkolny
Średni wynik:
13.17 pkt / 59.86%
2024-02-16

Inne zagadnienia z tej lekcji