Równoważność

Równoważność zdań p i q jest to zdanie orzekające, że zdania p i q mają tę samą wartość logiczną. Równoważność zdań p i q wypowiadamy w następujący sposób: p wtedy i tylko wtedy gdy q, a zapisujemy p ⇔ q.

Równoważność zdań p i q można zapisać w poniższej tabeli dla wszystkich przypadków:

p	q	p ⇔ q
0	0	1
0	1	0
1	0	0
1	1	1

Zdania równoważne są to więc zdania mające tę samą wartość logiczną.

Mówiąc inaczej zdanie równoważne to takie zdanie, którego człony mają taką samą wartość logiczną.

Przykłady

A oto przykłady równoważności zdań. Szczególnie ciekawy wydaje się ostatni z przykładów.

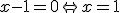$x-1=0\Leftright x=1$ .
Zmienna x jest liczbą pierwszą i mniejszą od 6 i większą od 3 wtedy i tylko wtedy, gdy x = 5.
Mleko jest białe wtedy i tylko wtedy, gdy 1+1 = 3 (jest to zdanie fałszywe).
Pójdę na spacer wtedy i tylko wtedy, gdy przestanie padać deszcz, tzn. „jeżeli przestanie padać, to pójdę na spacer” oraz „jeżeli pójdę na spacer, to przestanie padać”.
(10<100) ⇔ (100<1000).
W słowie „równoważność” jest 5 liter wtedy i tylko wtedy, gdy w tym słowie występuje tylko jedna samogłoska. Jest to zdanie prawdziwe, gdyż oba zdania składowe są fałszywe!
Zdanie p ⇔ q jest prawdziwe, wtedy i tylko wtedy gdy p i q są jednocześnie prawdziwe lub p i q są jednocześnie fałszywe.

Równoważność zdań p ⇔ q oznacza koniunkcję dwóch implikacji wzajemnie odwrotnych, czyli:

(p ⇔ q) ⇔ (p ⇒ q) ∧ (q ⇒ p).

Zaprzeczenie równoważności

Zaprzeczenie równoważności możemy zapisać w następujący sposób:

~ (p ⇔ q) ⇔ ~ [(p ⇒ q) ∧ (q ⇒ p)]

Skorzystamy z prawa de Morgana (zaprzeczenie koniunkcji):

~ (p ⇔ q) ⇔ ~ [(p ⇒ q) ∧ (q ⇒ p)] ⇔ [~ (p ⇒ q)] ∨ [~ (q ⇒ p)] ⇔ (p ⇒ ~ q) ∨ (q ⇒ ~ p)

Ostatni krok wymaga wyjaśnienia:

Negacja implikacji ~ (p ⇒ q) jest równoważna ~ (~ p ∨ q). Negacja alternatywy zgodnie z prawem de Morgana jest równoważna zapisowi ~ (~ p ∨ q) ⇔ p ∧ ~ q.