Alternatywa
Alternatywa w logice lub suma logiczna jest określona w następujący sposób:
Przykłady
Poniższa tabela zawiera przykłady sumy logicznej.
| p | q | p ∨ q | wartość logiczna p ∨ q |
|---|---|---|---|
| 5 jest liczbą nieparzystą. Zdanie prawdziwe. |
5 jest liczbą pierwszą. Zdanie prawdziwe. |
5 jest liczbą pierwszą lub nieparzystą. | Prawda |
Zdanie prawdziwe. |
Zdanie fałszywe. |
Prawda | |
| Słońce jest planetą. Zdanie fałszywe. |
Słońce jest pięć razy większe od Jowisza. Zdanie fałszywe. |
Słońce jest planetą lub jest pięć razy większe od Jowisza. | Fałsz |
Wyniki alternatywy zdań p i q, gdy p i q przybierają różne wartości logiczne, ilustruje poniższa tabela:
| p | q | p ∨ q |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Zatem alternatywa dowolnych zdań p i q jest fałszywa tylko w przypadku, gdy oba zdania p i q są fałszywe.
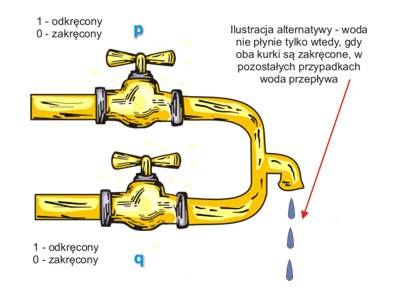
Jak zapamiętać wyniki alternatywy? Można wyobrazić sobie układ rur i zaworów, przez który przepływa woda tak, jak na powyższym rysunku. W rurze znajdują się równolegle dwa kurki: p i q. Stan kurka „odkręcony” niech oznacza wartość logiczną 1, „zakręcony” - wartość logiczną 0. Przepływ wody przez rurę realizuje alternatywę stanów kurków. Opisany przykład został zilustrowany na poniższym rysunku.
Pytania
Czy alternatywa (suma logiczna) znajduje zastosowanie w praktyce?
Najlepszym przykładem jest wykorzystanie alternatywy w informatyce przez programistów. W operacjach na bitach stosuje się alternatywę „OR” („LUB”), dla której operatorem jest najczęściej „|”, a także alternatywa wykluczająca (bitowa różnica symetryczna) „XOR” („ALBO”), dla której stosuje się najczęściej operator „^”. Są to operacje dwuargumentowe.
Suma bitowa OR włącza tylko te bity, które włączone są przynajmniej w jednym z argumentów.
| a | b | a | b |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Operacja bitowa XOR powoduje włączenie tylko tych bitów, które są różne w obu argumentach.
| a | b | a ^ b |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Przykład OR: 10001101 | 10101010 = 10101111
Przykład XOR: 10001101 ^ 10101010 = 00100111
Jeżeli włączysz tryb programisty w kalkulatorze systemowym Windows, możesz poćwiczyć powyższe operacje.
Czy jest alternatywa (suma logiczna) w Excelu?
Tak. To prosta i często wykorzystywana formuła, która w polskiej wersji językowej Excela nosi nazwę „=LUB”. Jako argumenty podajemy warunki logiczne. Jeżeli co najmniej jeden warunek jest spełniony, funkcja ta zwróci prawdę, w przeciwnym razie fałsz.
Przykład:
- Wpisz w komórkę B2 wartość 0.
- Wpisz w komórkę B3 wartość 1.
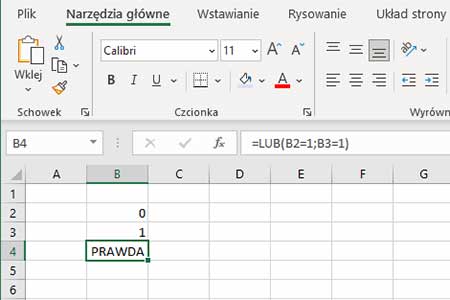
- Wpisz w komórkę B4 wyrażenie „=LUB(B2=1;B3=1)”
- Gdy naciśniesz ENTER, otrzymasz wynik PRAWDA. Dzieje się tak dlatego, że sprawdzasz, czy w komórce B2 i B3 jest wartość 1. A taka wartość jest wpisana w co najmniej jednej komórce.
- Zmień teraz wartość komórki B3 na inną niż 1. Otrzymasz wówczas wartość FAŁSZ w komórce B4.
Zadania z rozwiązaniami

Zadanie nr 1.
Określ wartość logiczną zdań:
A. \((1<3) \vee (2<6)\)
B. \((3<1) \vee (2<6)\)
C. \((3<1) \vee (6<2)\)
D. \((1<3) \vee (6<2)\)

Zadanie nr 2.
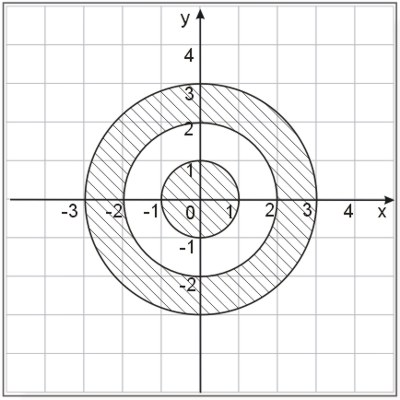
Zapisz za pomocą wzoru zbiór przedstawiony na rysunku (zakreskowane pole).
Powiązane materiały
© medianauka.pl, 2008-05-28, A-43
Data aktualizacji artykułu: 2023-02-07

 Zdanie logiczne
Zdanie logiczne Negacja
Negacja Koniunkcja
Koniunkcja Równoważność zdań
Równoważność zdań Elementy logiki cz.1
Elementy logiki cz.1