Funkcja złożona
Niech dziedziną funkcji \(f\) będzie zbiór \(A\), a przeciwdziedziną zbiór \(B\). Niech dziedziną funkcji \(g\) będzie zbiór, który zawiera przeciwdziedzinę funkcji \(f\), a przeciwdziedziną zbiór \(C\). Istnieje funkcja \(h:A \rightarrow C\) określona w następujący sposób: \(h(x)=g(f(x))\). Funkcję taką nazywamy funkcją złożoną lub superpozycją funkcji \(f\) i \(g\).
Złożenie funkcji \(f\) z \(g\) oznaczamy przez \(g(f(x))\) lub \((g \circ f)(x)\).
Funkcję \(f\) nazywamy funkcją wewnętrzną, natomiast funkcję \(g\) nazywamy funkcją zewnętrzną.
Przykłady
Oto przykłady funkcji złożonych:
- Funkcja \(y=\sin 3x\): funkcja \(f(x)=3x\) jest tutaj funkcją wewnętrzną, natomiast funkcja sinus — zewnętrzną.
- Funkcja \(y=\sin^2{x}\): funkcją wewnętrzną jest tutaj funkcja \(f(x)=\sin{x}\), a zewnętrzną — funkcja kwadratowa.
- Funkcja \(y=3\log^2{x}+\log{x-1}\): funkcja wewnętrzna to \(f(x)=\log{x}\), a zewnętrzna to \(g(u)=3u^2+u-1\).
Identyfikacja funkcji złożonej i rozkład na funkcję wewnętrzną i zewnętrzna ma duże znaczenie przy obliczaniu pochodnej funkcji.
Nie zawsze możemy też złożyć dwie funkcje. Zauważmy, że w trzecim przykładzie mamy określoną funkcję \((g \circ f)(x)\), ale nie możemy już dokonać złożenia \((f \circ g)(x)\), z takiego powodu, że przeciwdziedzina funkcji \(g\) (zbiór liczb rzeczywistych) nie zawiera się w dziedzinie funkcji \(f\) (zbiór liczb rzeczywistych dodatnich).
Zadania z rozwiązaniami

Zadanie nr 1.
Dane są funkcje:
- \(f(x)=x^2, g(x)=3x+1\)
- \(f(x)=3x+1, g(x)=\log{x}\)
- \(f(x)=2x,\ x> 0, g(x)=\log{x}\)
Znaleźć złożenie funkcji: \((g\circ f)(x)\) i \((f\circ f)(x)\).

Zadanie nr 2.
Dane są funkcje:
- \(f(x)=\cos{x},\ g(x)=\sqrt{x}\)
- \(f(x)=\sin{x},\ g(x)=x^2\)
- \(f(x)=\log{x},\ g(x)=\sqrt{x}\)
Znaleźć złożenie tych funkcji: \((g\circ f)(x)\) i \((f\circ g)(x)\).
Powiązane materiały
© medianauka.pl, 2009-05-21, A-211
Data aktualizacji artykułu: 2023-04-08

 Funkcja odwrotna i tożsamościowa
Funkcja odwrotna i tożsamościowa Funkcja odwrotna i funkcja złożona
Funkcja odwrotna i funkcja złożona Funkcja
Funkcja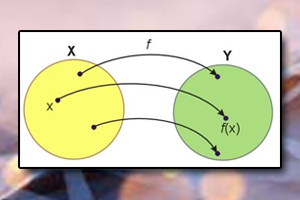 Funkcja różnowartościowa
Funkcja różnowartościowa