Podzbiory

Zawieranie się zbiorów

Definicja

Jeżeli każdy element zbioru A należy do zbioru B , to mówimy, że zbiór A zawiera się w zbiorze B i oznaczamy: $A\subset B$ .

Zawieranie się zbioru A w zbiorze B można zilustrować tak jak na poniższym rysunku.

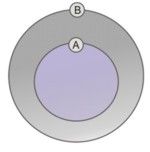
Przykład

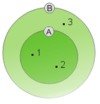
A={1,2}, B={1,2,3}, $A\subset B$ , ponieważ elementy "1" i "2" zbioru A są elementami zbioru B. Zbiór B nie zawiera się w zbiorze A, bo element "3" nie jest elementem zbioru A. Przykład ten został przedstawiony na ilustracji.
Zbiór {a,g} zawiera się w zbiorze {a,h,g}.
Zbiór kwadratów zawiera się w zbiorze prostokątów, a zbiór prostokątów zawiera się w zbiorze czworokątów.

Podzbiór

Jeżeli $A\subset B$ , to zbiór A nazywamy podzbiorem zbioru B, a zbiór B nazywamy nadzbiorem zbioru A.

Z definicji zawierania się zbioru w zbiorze wynika, że:

Ø (zbiór pusty jest podzbiorem każdego innego zbioru),
$A\subset A$ (zbiór A jest podzbiorem samego siebie).

Jeżeli zbiór A nie jest podzbiorem zbioru B, to możemy użyć zapisu A⊄B.

Zadanie

Znaleźć wszystkie podzbiory zbioru A={a,b,c}.

Rozwiązanie: {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, A, Ø.

Równość zbiorów

Zbiory A i B są równe i zapisujemy A=B wtedy i tylko wtedy, gdy każdy element zbioru A jest elementem zbioru B i każdy element zbioru B jest elementem zbioru A.

Przykład

Dla przykładu zbiory {1,2} oraz {2,1} są równe, gdyż zawierają dokładnie takie same elementy (kolejność wypisywania elementów zbioru nie ma znaczenia).

Ćwiczenia

Ćwiczenia interakcyjne pomogą przygotować się na sprawdzian, test, egzamin, a ponadto usystematyzują wiedzę z danej dziedziny. To także świetny trening do matury. Wiele ćwiczeń to dobre zadania maturalne.

ĆWICZENIA

Podzbiory

Filmy

Podzbiór - definicja i przykłady.

Zadania z rozwiązaniami

Zadanie nr 1.

Znaleźć wszystkie dwuelementowe podzbiory zbioru A={1,2,3,4}:

Pokaż rozwiązanie zadania.

Inne zagadnienia z tej lekcji

Zbiór

Zbiór jest pojęciem pierwotnym, a więc nie definiujemy go. Pojęciem pierwotnym jest także element zbioru.

Suma zbiorów

Zbiór elementów, z których każdy należy do zbioru A lub B nazywamy sumą zbioru A i B

Różnica zbiorów

Zbiór elementów, z których każdy należy do zbioru A i nie należy do B nazywamy różnicą zbioru A i B

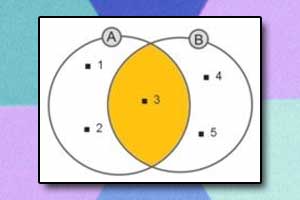Iloczyn zbiorów

Co to jest iloczyn zbiorów? Zbiór elementów, z których każdy należy do zbioru A i do B nazywamy iloczynem zbioru A i B.

Iloczyn kartezjański zbiorów

Iloczynem kartezjańskim zbiorów A i B nazywamy zbiór wszystkich par uporządkowanych (x,y) takich, że x in A i y in B i oznaczamy A×B. Wynikiem tego działania jest wektor.

Test wiedzy

Sprawdź swoje umiejętności z materiału zawartego w tej lekcji.