Suma zbiorów

Działania na zbiorach są wykonalne. W naszym kursie określimy sumę, różnicę, iloczyn oraz iloczyn kartezjański zbiorów. W tym artykule zajmujemy się sumą zbiorów.

Definicja

Zbiór elementów, z których każdy należy do zbioru A lub B nazywamy sumą zbioru A i B i oznaczamy: A∪B.

Znak sumy zbiorów w matematyce to symbol ∪.

Sumę zbiorów (dodawanie zbiorów) można zilustrować rysunkiem. Kolorem zielonym zaznaczono sumę zbiorów A i B.

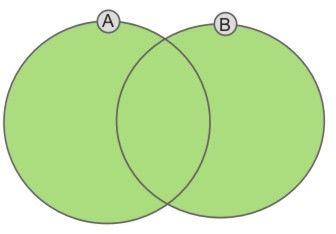
Przykłady

Przykład

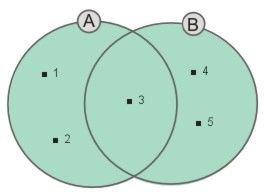
Zbiory A i B zostały określone następująco: A={1,2,3} i B={3,4,5}.

Zgodnie z definicją sumy zbiorów A∪B={1,2,3,4,5}. Wspólny element "3" należy do obu zbiorów. Należy także do sumy tych zbiorów.
Przykład ten został przedstawiony na ilustracji obok.

Tworząc sumę zbiorów wypisujemy wszystkie elementy pierwszego i drugiego zbioru, a te elementy, które należą i do jednego i do drugiego zbioru wypisujemy tylko raz.

Przykład

A oto inne przykłady sumy zbiorów:

{a}∪{a}∪{a}∪{a}={a}
{m}∪{a}∪{m}∪{a}={m, a}
A={1,2,3,4,5,6,7,8,9}, B={3,5}, A∪B=A

Własności sumy zbiorów

Suma zbiorów jest przemienna, czyli:

A∪B = B∪A

Zachodzi też łączność sumy, czyli:

(A∪B)∪C = A∪(B∪C)

Kalkulator - działania na zbiorach

W tym miejscu możesz obliczyć sumę, różnicę i iloczyn (część współną) zbiorów skończonych. Podaj elementy dwóch zbiorów (co najmniej jeden). Poszczególne elementy rozdzielaj przecinkami.

Wpisz dane:

Zbiór A={

}

Zbiór B={

}

Rozwiązanie:

Ćwiczenia

Ćwiczenia interakcyjne pomogą przygotować się na sprawdzian, test, egzamin, a ponadto usystematyzują wiedzę z danej dziedziny. To także świetny trening do matury. Wiele ćwiczeń to dobre zadania maturalne.

Ćwiczenia
Wykonaj ćwiczenia związane z tematem

Suma zbiorów

Filmy

Działania na zbiorach.

Zadania z rozwiązaniami

Zadania związane z tematem:
Suma zbiorów

Zadanie - suma zbiorów, metoda graficzna
Zakreskować sumę zbiorów A, B i C, zilustrowanych na poniższym rysunku:
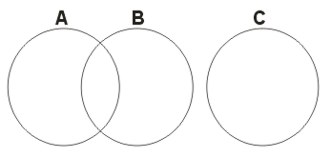
zbiory

Pokaż rozwiązanie zadania

Zadanie - suma zbiorów
Znaleźć sumę zbiorów:
a) {1,2,3,4}, {3,4,5,6}, {a}
b) {0}, {1}, {0,1}
c) {a}, {a,d}, {a,b,c}

Pokaż rozwiązanie zadania

Zadanie - znaleźć sumę zbiorów
Znaleźć sumę zbiorów: $\lbrace x\in R:x>-1 \rbrace \cup \lbrace x\in R:x<1 \rbrace$

Pokaż rozwiązanie zadania

Inne zagadnienia z tej lekcji

Zbiór

Zbiór jest pojęciem pierwotnym, a więc nie definiujemy go. Pojęciem pierwotnym jest także element zbioru.

Podzbiory

Pojęcie podzbioru, zawierania się zbiorów oraz równości zbiorów

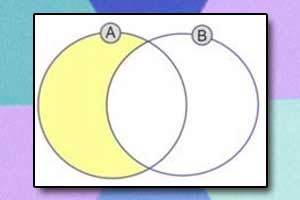Różnica zbiorów

Zbiór elementów, z których każdy należy do zbioru A i nie należy do B nazywamy różnicą zbioru A i B

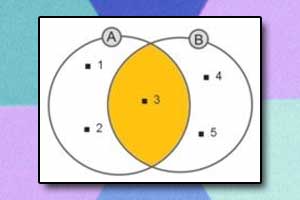Iloczyn zbiorów

Co to jest iloczyn zbiorów? Zbiór elementów, z których każdy należy do zbioru A i do B nazywamy iloczynem zbioru A i B.

Iloczyn kartezjański zbiorów

Iloczynem kartezjańskim zbiorów A i B nazywamy zbiór wszystkich par uporządkowanych (x,y) takich, że x in A i y in B i oznaczamy A×B. Wynikiem tego działania jest wektor.

Test wiedzy

Sprawdź swoje umiejętności z materiału zawartego w tej lekcji.