Iloczyn zbiorów
Co to jest część wspólna, zwana także iloczynem zbiorów lub przekrojem zbiorów albo ich przecięciem?
Symbol iloczynu zbiorów to ∩.
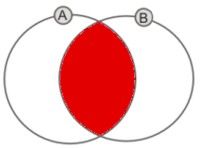
Iloczyn zbiorów można zilustrować za pomocą rysunku. Kolorem czerwonym zaznaczono przekrój zbiorów A ∩ B. Iloczyn zbiorów to nic innego jak część wspólna zbiorów.
Przykłady
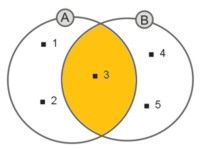
Zbiory A i B zostały określone następująco:
A = {1, 2, 3} i B = {3, 4, 5}. Zgodnie z definicją iloczynu zbiorów A ∩ B = {3}. Przykład ten został przedstawiony na ilustracji.
Tworząc iloczyn zbiorów, wypisujemy wszystkie elementy wspólne obu zbiorów.
Przykład
A oto inne przykłady różnicy zbiorów:
- {a, b, c} ∩ {c} = {c};
- {a, b, c} ∩ {a, b, c} = {a, b, c};
- {a, b, c} ∩ {d, e, f} = Ø;
- {„to”} ∩ {„ot”} = Ø (mamy tutaj zbiory jednoelementowe o różnych elementach);
- iloczynem zbioru liczb całkowitych większych od 5 i zbioru liczb całkowitych mniejszych od 10 jest zbiór {6, 7, 8, 9}.
Własności części wspólnej zbiorów
Iloczyn zbiorów jest przemienny, czyli:
Iloczyn zbiorów jest łączny, czyli:
Zachodzą również następujące prawa:
- rozdzielności iloczynu względem sumy: (A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C);
- rozdzielności sumy względem iloczynu: (A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C).
Zbiory rozłączne
Definicja
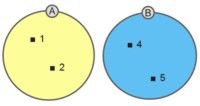
Zbiory rozłączne można zilustrować następująco:
Prawa de Morgana dla zbiorów
Dopełnienie sumy zbiorów jest równe części wspólnej ich dopełnień: (A ∪ B)' = A' ∩ B'.
Dopełnienie części wspólnej zbiorów jest równe sumie ich dopełnień: (A ∩ B)' = A' ∪ B'.

Kalkulator — działania na zbiorach
W tym miejscu możesz obliczyć sumę, różnicę i część wspólną zbiorów skończonych. Podaj elementy dwóch zbiorów (co najmniej jeden). Poszczególne elementy rozdzielaj przecinkami.
Wpisz dane:Pytania
Czy zbiory można mnożyć?
Iloczyn to wynik mnożenia. Nie mówimy jednak o typowym działaniu mnożenia w przypadku zbiorów. Dla zbiorów określa się dwa rodzaje iloczynów zbiorów. Pierwszym z nich jest działanie zdefiniowane w tym artykule, a drugim jest tak zwany iloczyn kartezjański, który został omówiony w odrębnym artyklule, do którego link znajdziesz poniżej.
Zadania z rozwiązaniami

Zadanie nr 1.
Znaleźć iloczyn zbiorów:
\(\lbrace x\in \mathbb{R}:x\geq -1 \rbrace \cap \lbrace x\in \mathbb{R}:x<1 \rbrace\)

Zadanie nr 2.
Oblicz:
a) \(\lbrace 5,6,7,8\rbrace \cap \lbrace 3,4,5\rbrace \)
b) \( \lbrace a,c\rbrace \cap \lbrace 1,2\rbrace \)
c) \(\lbrace a, b, c\rbrace \cap \lbrace abc\rbrace \)
d) \(\lbrace 1, 2, 3\rbrace \cap \lbrace 1, 2\rbrace \)
e) \(\mathbb{N}\cap \mathbb{Z}\)

Zadanie nr 3.
Zakreskować iloczyn zbiorów zilustrowanych na poniższym rysunku:
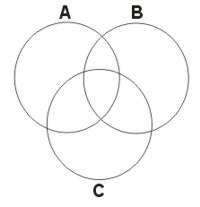
a) \(A\cap B \cap C\)
b) \(A\cap C\)
c) \((A\cup B) \cap C\)
Powiązane materiały
 Iloczyn zbiorów
Iloczyn zbiorów Zbiory — quiz
Zbiory — quizFilmy
© medianauka.pl, 2008-07-14, A-65
Data aktualizacji artykułu: 2024-05-07

 Zbiór
Zbiór Podzbiory
Podzbiory Suma zbiorów
Suma zbiorów Różnica zbiorów
Różnica zbiorów Iloczyn kartezjański
Iloczyn kartezjański Pojęcie zbioru i działania na zbiorach
Pojęcie zbioru i działania na zbiorach Działania na zbiorach — quiz
Działania na zbiorach — quiz