Zbiór
Zbiór jest pojęciem pierwotnym, a więc nie definiujemy go. Czasami, zamiast mówić „zbiór” będziemy używać pojęcia „mnogość”. Pojęciem pierwotnym jest także element zbioru.
Zbiory oznaczamy dużymi literami alfabetu, elementy zbioru — małymi literami.
Używamy też następujących symboli:
\(\in\) — czytamy: należy do;
\(\notin\) — czytamy: nie należy do;
Zapis: \(a\in A\) czytamy: „element \(a\) należy do zbioru A” lub „\(a\) jest elementem zbioru A”.
Zapis: \(a\notin A\) czytamy: „element \(a\) nie należy do zbioru A” lub „\(a\) nie jest elementem zbioru A”.
Zbiór pusty
Zbiór skończony i nieskończony
Przykłady
- Zbiór liczb naturalnych jest przykładem zbioru nieskończonego.
- Zbiór wszystkich ułamków zwykłych jest przykładem zbioru nieskończonego.
- \(A=\lbrace 1, 2, 3, 4, 5, 6, 7, 8, 9, 10\rbrace\) jest zbiorem skończonym, dziesięcioelementowym, jego elementami są liczby naturalne mniejsze od 11.
Zbiór A z powyższego przykładu można też przedstawić graficznie w postaci pętli.
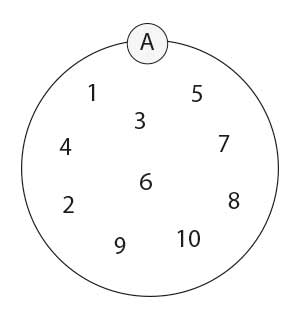
Zbiór możemy określić także poprzez wypisanie elementów w nawiasach klamrowych lub poprzez własność \(W(x)\). Zapisujemy go wówczas jako:
\(\lbrace x\in A:W(x)\rbrace\).
Dla przykładu zbiór wszystkich liczb rzeczywistych większych od 1 i mniejszych od 10 możemy zapisać jako \(\lbrace x \in \mathbb{R}: 1<x<10\rbrace \).
Równoliczność zbiorów
Jeżeli zbiory A i B mają po tyle samo elementów, to mówimy, że są równoliczne.
Łatwo sprawdzić równoliczność zbiorów skończonych. Wystarczy policzyć ich elementy. Dla przykładu zbiór \(A=\lbrace 1, 2, 3, 4, 5, 6, 7, 8, 9, 10\rbrace\) jest równoliczny ze zbiorem \(B=\lbrace a, b, c, d, e, f, g, h, i, j\rbrace \), ponieważ oba zbiory mają po 10 elementów.
Jak sprawdzić równoliczność dwóch zbiorów nieskończonych A i B? Postępujemy w takim przypadku w następujący sposób:
Tworzymy pary elementów tych zbiorów tak, aby:
- pierwsze elementy par były elementami zbioru A, nie pomijamy przy tym żadnego elementu zbioru A (mówimy, że elementy wyczerpują ten zbiór);
- drugie elementy par były elementami zbioru B, które wyczerpują ten zbiór.
Jeżeli każde dwie różne pary nie mają tego samego poprzednika ani tego samego następnika, to mamy pewność, że zbiory A i B są równoliczne.
Przykład
Sprawdźmy, czy zbiór liczb naturalnych jest równoliczny ze zbiorem liczb naturalnych parzystych. Zgodnie z powyższą zasadą bierzemy każdy z elementów pierwszego zbioru oraz z drugiego zbioru i tworzymy pary: (1, 2), (2, 4), (3, 6), (4, 8), (5, 10), ... (kolejna liczba naturalna, kolejna liczba parzysta). Ponieważ każdy element tych zbiorów wykorzystujemy tylko raz, tworząc pary, udowodniliśmy, że zbiory te są równoliczne.
Moc zbioru
Jeżeli dwa zbiory są równoliczne, to mówimy, że mają tę samą moc (liczbę kardynalną). Moc zbioru \(A\) oznaczamy następująco: \(|A|\) lub \(\overline{\overline{A}}\). Dla zbiorów skończonych liczba kardynalna to nic innego jak liczba jego elementów.
Ciekawostki
- Intuicja podpowiada nam, że liczb naturalnych jest dwa razy więcej niż liczb parzystych, ale tak nie jest, co wyżej udowodniliśmy. Liczb naturalnych jest dokładnie tyle samo co liczb parzystych! Podobnie można wykazać, że prosta ma tyle samo punktów co płaszczyzna!
 Można wykazać, że zbiór liczb naturalnych nie jest równoliczny ze zbiorem liczb rzeczywistych. To wydaje się na pierwszy rzut oka zdroworozsądkowe, ale czy aby na pewno? To przecież oznacza, że liczb rzeczywistych jest więcej niż naturalnych. Ile ich jest? Nieskończenie wiele. Czy wszystko w porządku? Przecież liczb naturalnych również jest nieskończenie wiele! „Nieskończenie wiele” i „nieskończenie wiele” to nie to samo? Badanie mocy zbiorów (liczb kardynalnych) nieskończonych jest ciekawym doświadczeniem i wprawia w zdumienie. Rzeczywiście okazuje się, że „nieskończoności” różnią się od siebie. Warto wiedzieć, że najmniejszą liczbą kardynalną nieskończoną jest moc zbioru liczb naturalnych.
Można wykazać, że zbiór liczb naturalnych nie jest równoliczny ze zbiorem liczb rzeczywistych. To wydaje się na pierwszy rzut oka zdroworozsądkowe, ale czy aby na pewno? To przecież oznacza, że liczb rzeczywistych jest więcej niż naturalnych. Ile ich jest? Nieskończenie wiele. Czy wszystko w porządku? Przecież liczb naturalnych również jest nieskończenie wiele! „Nieskończenie wiele” i „nieskończenie wiele” to nie to samo? Badanie mocy zbiorów (liczb kardynalnych) nieskończonych jest ciekawym doświadczeniem i wprawia w zdumienie. Rzeczywiście okazuje się, że „nieskończoności” różnią się od siebie. Warto wiedzieć, że najmniejszą liczbą kardynalną nieskończoną jest moc zbioru liczb naturalnych.- Podwaliny pod teorię mnogości stworzył niemiecki matematyk — Georg Cantor (1845-1918).
- Moc zbioru liczb naturalnych nazywamy alef zero i oznaczamy ℵ0.
Pytania
Jak wyznaczyć zbiór wartości funkcji?
Na to pytanie odpowiadamy w artykule: Wyznaczanie wartości i argumentów funkcji.
Zadania z rozwiązaniami

Zadanie nr 1.
Zapisz za pomocą określenia własności zbioru następujące zbiory liczb:
A. Zbiór liczb całkowitych większych od 1000.
B. Zbiór liczb naturalnych, podzielnych przez 15.
C. Zbiór liczb parzystych dodatnich.
D. Zbiór liczb nieparzystych.

Zadanie nr 2.
Wypisz elementy zbiorów:
\(A=\lbrace x\in \mathbb{Z}: -11<x<1 \rbrace\).
\(B=\lbrace x\in \mathbb{N}: 3|x \land x<15\rbrace\)
\(C=\lbrace p \in \mathbb{Z}: |p|\leq 4 \rbrace\)
\(D=\lbrace x \in \mathbb{R}: x^2=-1 \rbrace\)
\(E=\lbrace n\in \mathbb{N}: n^2 \rbrace\)
Powiązane materiały
 Zbiór
Zbiór Zbiory — quiz
Zbiory — quizFilmy
© medianauka.pl, 2008-07-09, A-61
Data aktualizacji artykułu: 2023-02-14

 Zbiór potęgowy
Zbiór potęgowy Podzbiory
Podzbiory Suma zbiorów
Suma zbiorów Różnica zbiorów
Różnica zbiorów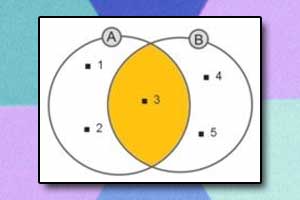 Iloczyn zbiorów
Iloczyn zbiorów Iloczyn kartezjański
Iloczyn kartezjański Pojęcie zbioru i działania na zbiorach
Pojęcie zbioru i działania na zbiorach Prawa de Morgana
Prawa de Morgana Liczby naturalne
Liczby naturalne Przedziały liczbowe
Przedziały liczbowe Czy liczb całkowitych jest więcej od liczb naturalnych?
Czy liczb całkowitych jest więcej od liczb naturalnych? Czy liczb całkowitych jest więcej od liczb naturalnych?
Czy liczb całkowitych jest więcej od liczb naturalnych? Działania na zbiorach — quiz
Działania na zbiorach — quiz