Wartości i argumenty funkcji
Przy definiowaniu pojęcia funkcji pojawia się pojęcie wartości i argumentu funkcji.
Wartość funkcji
W funkcji zdefiniowanej jako \(f(x)= x\rightarrow y\), gdzie \(x\in X, y\in Y\) wartość funkcji jest to dowolny element \(y\), a zbiór wartości funkcji jest to zbiór \(Y\). Jest to zbiór takich \(y\in Y\), dla których istnieje \(x\in X\) takie, że \(y=f(x)\). Zbiór wartości funkcji to przeciwdziedzina tej funkcji.
Aby wyznaczyć wartość danej funkcji, musimy mieć określony argument funkcji oraz samą funkcję. Wyznaczenie wartości polega zwykle na podstawieniu argumentu funkcji do wzoru, który określa tę funkcję. Oto prosty przykład:
Przykłady
Dana jest funkcja \(f(x)=\frac{1}{x-3}\). Wyznaczyć wartość funkcji dla argumentu \(x=4\).
Wyznaczenie wartości polega więc na podstawieniu do wzoru za \(x\) liczby 4.
\(f(4)=\frac{1}{4-3}=\frac{1}{1}=1\)
A oto kilka innych wartości funkcji:
- \(f(0)= \frac{1}{0-3}=-\frac{1}{3}\)
- \(f(-3)= \frac{1}{-3-3}=-\frac{1}{6}\)
Argument funkcji
W funkcji zdefiniowanej jako \(f(x)= x\rightarrow y\), gdzie \(x\in X, y\in Y\) argument funkcji lub zmienna niezależna jest to dowolny element \(x\), a zbiór argumentów funkcji jest to zbiór \(X\). Zbiór zmiennych niezależnych funkcji to dziedzina tej funkcji.
Przy wyznaczaniu argumentu funkcji musimy oprócz samej funkcji znać jej wartość.
Przykłady
Wyznaczyć argument funkcji \(f(x)=x+8\) wiedząc, że \(f(x)=3\).
Podstawiamy więc wartość funkcji do wzoru funkcji i otrzymujemy równanie:
\(3=x+8\)
\(-x=5\)
\( x=-5\)
Zatem funkcja przyjmuje wartość 3 dla argumentu równego -5.
Nie zawsze funkcja jest wyrażona za pomocą zmiennej \(x\). W fizyce na przykład korzystamy z pojęcia funkcji, przyjmując za zmienne różne wielkości fizyczne.
Przykłady
Obliczmy drogę, jaką ciało przebyło w ciągu 1 s w ruchu jednostajnie przyspieszonym ze stałym przyspieszeniem \(a=2\ \frac{m}{s^2}\) ze stanu spoczynku. Droga przebyta przez to ciało wyrażona jest wzorem: \(s=\frac{1}{2}at^2\), gdzie \(a\) — przyspieszenie i jest wartością stałą.
Widzimy, że zmienną niezależną (argumentem funkcji) jest czas \(t\), a zmienną zależną jest droga \(s\).
Mówimy, że droga jest funkcją czasu w ruchu jednostajnie przyspieszonym.
Zatem musimy obliczyć wartość funkcji:
\(s(t)\), dla \( t=1\ s\)
\(s (1\ s)= \frac{1}{2} \cdot 2 \cdot \frac{m}{s^2} \cdot (1\ s)^2=1\ m\)
Zadania z rozwiązaniami

Zadanie nr 1.
Dana jest funkcja \(f(x)=\frac{x-3}{x^2+4}+x-1\)
Obliczyć:
a) \(f(1)\)
b) \(f(0)\)
c) \(f(-2)\)
d) \(f(\frac{1}{2})\).

Zadanie nr 2 — maturalne.
Funkcja f określona jest wzorem \(f(x)=\frac{2x^3}{x^6+1}\) dla każdej liczby rzeczywistej \(x\). Wtedy \(f(-\sqrt[3]{3})\) jest równa:
A. \(-\frac{\sqrt[3]{9}}{2}\)
B. \(-\frac{3}{5}\)
C. \(\frac{3}{5}\)
D. \(\frac{3}{5}\)

Zadanie nr 3 — maturalne.
Na rysunku przedstawiono wykres funkcji \(f\).
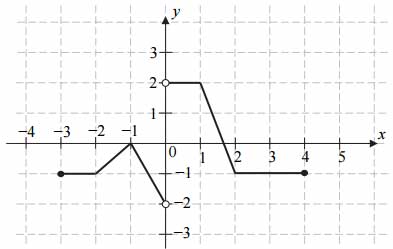
Zbiorem wartości funkcji \(f\) jest
A. \((-2,2)\)
B. \([-2,2)\)
C. \([-2,2]\)
D. \((-2,2]\)

Zadanie nr 4 — maturalne.
Funkcja kwadratowa określona jest wzorem \(f(x)=x^2+x+c\). Jeżeli \(f(3)=4\), to:
A. \(f(1)=-6\)
B. \(f(1)=0\)
C. \(f(1)=6\)
D. \(f(1)=18\)

Zadanie nr 5 — maturalne.
Do wykresu funkcji, określonej dla wszystkich liczb rzeczywistych wzorem \(y=-2^{x-2}\), należy punkt:
A. \(A=(1,-2)\)
B. \(B=(2,-1)\)
C. \(C=(1,\frac{1}{2})\)
D. \(D=(4,4)\)

Zadanie nr 6 — maturalne.
Punkt \(A=(\frac{1}{3},-1)\) należy do wykresu funkcji liniowej \(f\) określonej wzorem \(f(x)=3x+b\). Wynika stąd, że
A. \(b=2\)
B. \(b=1\)
C. \(b=-1\)
D. \(b=-2\)

Zadanie nr 7 — maturalne.
Funkcja \(f\) jest określona wzorem \(f(x)=\frac{x^2}{(2x-2)}\) dla każdej liczby rzeczywistej \(x \neq 1\). Wtedy dla argumentu \(x=\sqrt{3}-1\) wartość funkcji \(f\) jest równa
A. \(\frac{1}{\sqrt{3}-1)}\)
B. \(-1\)
C. \(1\)
D. \(\frac{1}{(\sqrt{3}-2)}\)

Zadanie nr 8 — maturalne.
Do wykresu funkcji \(f\) określonej dla każdej liczby rzeczywistej \(x\) wzorem \(f(x)=3^x-2\) należy punkt o współrzędnych
A. \((-1,-5)\)
B. \((0,-2)\)
C. \((0,-1)\)
D. \((2,4)\)

Zadanie nr 9 — maturalne.
Funkcja liniowa \(f\) przyjmuje wartość \(2\) dla argumentu \(0\), a ponadto \(f(4)-f(2)=6\). Wyznacz wzór funkcji \(f\).

Zadanie nr 10 — maturalne.
Na rysunku przedstawiono wykres funkcji \(f\).
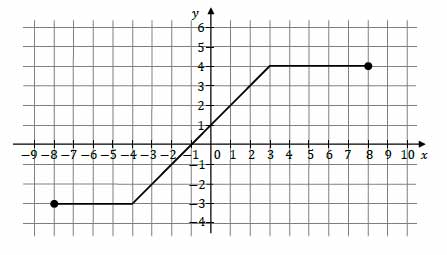
Iloczyn \(f(-3)\cdot f(0)\cdot f(4)\) jest równy
A. (-12)
B. (-8)
C. 0
D. 16

Zadanie nr 11 — maturalne.
Miejscem zerowym funkcji liniowej \(f\) określonej wzorem \(f(x)=\frac{1}{3}(x+3)+5\) jest liczba
A. (-3)
B. \(\frac{9}{2}\)
C. 5
D. 12
Powiązane materiały
© medianauka.pl, 2009-04-29, A-192
Data aktualizacji artykułu: 2023-04-01

 Funkcja
Funkcja Wyznaczanie dziedziny funkcji
Wyznaczanie dziedziny funkcji Funkcja — podstawowe pojęcia
Funkcja — podstawowe pojęcia Ekstremum funkcji
Ekstremum funkcji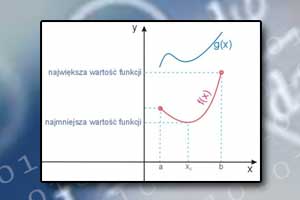 Największa i najmniejsza wartość funkcji
Największa i najmniejsza wartość funkcji