Dziedzina funkcji
Co to jest dziedzina funkcji? Dziedzina jest zbiorem argumentów funkcji. Jeśli dziedzina nie jest jawnie zapisana przy określeniu funkcji (a tak zazwyczaj jest) przyjmujemy, że jest nią zbiór wszystkich liczb, dla których spełniona jest prawa strona równości \(y=f(x)\). Dziedzinę oznaczamy symbolem \(D_{f}\).
Wyznaczanie dziedziny funkcji
Jak wyznaczyć dziedzinę funkcji? Aby wyznaczyć dziedzinę funkcji, należy pamiętać głównie o trzech zasadach:
- Wartość wyrażenia w mianowniku musi być różna od zera.
- Wartość wyrażenia pod pierwiastkiem parzystego stopnia musi być większe bądź równe zero.
- Wyrażenie logarytmowane musi być dodatnie.
Brak zapisu dziedziny oznacza, że dopuszczamy do rozważań wszystkie liczby rzeczywiste.
Obliczanie dziedziny funkcji prześledzimy na przykładach.
Zadanie 1
Wyznaczyć dziedzinę funkcji \(x \rightarrow y=\frac{x}{x+5}\).
Mianownik wyrażenia po prawej stronie równości musi być różny od zera, a więc \(x+5 \neq 0\), zatem \(x \neq -5\).
Odpowiedź: \(D_{f}=R \backslash \lbrace -5 \rbrace\)
Zadanie 2
Wyznaczyć dziedzinę funkcji \(f(x)=\sqrt{-x+1}\)
Wyrażenie pod pierwiastkiem musi być większe lub równe 0, a więc:
\(-x+1 \geq 0\)
\(-x \geq -1\)
\(x \leq 1\)
Odpowiedź: \(D_{f}=(- \infty; 1\rangle\).
(wynik zapisaliśmy za pomocą przedziału liczbowego).
Zadanie 3
Wyznaczyć dziedzinę funkcji:
\(f(x)=\sqrt{\frac{1}{x^2-1}}\)
Po pierwsze całe wyrażenie pod pierwiastkiem nie może być liczbą ujemną, a po drugie: wyrażenie w mianowniku musi być różne od zera.
Pierwszy warunek: \(\frac{1}{x^2-1} \geq 0\).
Ponieważ licznik jest dodatni, to aby cały ułamek był nieujemny, mianownik również musi być nieujemny.
\(x^2-1 \geq 0\).
Stosujemy wzór skróconego mnożenia i otrzymujemy: \((x-1)(x+1)\geq 0\).
Iloczyn dwóch liczb jest nieujemny, jeżeli oba czynniki są dodatnie lub oba są ujemne. Otrzymujemy zatem układy równań:
\(\begin{cases} x+1 \geq 0\\ x-1 \geq 0 \end{cases} \qquad lub \qquad \begin{cases} x+1 \leq 0\\x-1 \leq 0 \end{cases}\)
Zatem:
\(\begin{cases} x \geq -1\\ x \geq 1 \end{cases} \qquad lub \qquad \begin{cases} x \leq -1\\x \leq 1 \end{cases}\)
Mamy zatem rozwiązanie:
\(x \geq 1 \qquad lub \qquad x \leq -1\)
Możemy to zapisać za pomocą przedziału liczbowego: \((- \infty; -1\rangle \cup \langle 1; \infty)\).
Nie jest to jeszcze jednak dziedzina naszej funkcji, gdyż mamy jeszcze do zbadania drugi warunek, mianowicie — mianownik ułamka musi być różny od zera, a więc \(x^2-1 \neq 0\), czyli \(x^2 \neq 1, \qquad x \neq 1 \vee x\neq -1\).
Musimy więc uwzględnić ten wynik i otrzymujemy ostateczną odpowiedź:
Odpowiedź: \(D_{f}=(- \infty; -1) \cup (1; \infty)\)
Dziedziny różnych funkcji
W poniższej tabeli zostały zawarte przydatne informacje w wyznaczaniu dziedzin różnych funkcji.
| Dziedzina | |
|---|---|
| Dziedzina funkcji liniowej. | \(\mathbb{R}\) |
| Dziedzina funkcji kwadratowej. | \(\mathbb{R}\) |
| Dziedzina funkcji z pierwiastkiem. | Wartość pod pierwiastkiem musi być większa lub równa zeru. |
| Dziedzina funkcji logarytmicznej \(y=\log_a{x}\). |
|
| Dziedzina funkcji wymiernej \(y=\frac{g(x)}{h(x)}\) | \(h(x)\neq 0\), czyli wyznaczamy miejsca zerowe (pierwiastki) wielomianu h(x), a następnie wyłączamy je ze zbioru liczb rzeczywistych. |
| Dziedzina funkcji wykładniczej \(y=a^x\). |
|
| Dziedzina funkcji dwóch zmiennych . | Stosujemy te same zasady określania zbioru argumentów funkcji łącznie dla każdej ze zmiennych. |
Zadania z rozwiązaniami

Zadanie nr 1.
Wyznaczyć dziedzinę funkcji
a) \(f(x)=\sqrt{x^2-3x}\)
b) \(f(x)=log_{x-1}{x+1}\)
Powiązane materiały
© medianauka.pl, 2009-04-29, A-193
Data aktualizacji artykułu: 2023-04-01

 Funkcja
Funkcja Wartości i argumenty funkcji
Wartości i argumenty funkcji Funkcja — podstawowe pojęcia
Funkcja — podstawowe pojęcia Wykres funkcji
Wykres funkcji Miejsce zerowe funkcji
Miejsce zerowe funkcji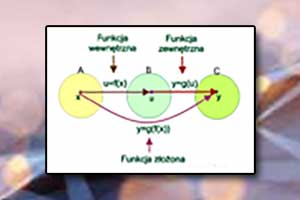 Funkcja złożona
Funkcja złożona