Największa i najmniejsza wartość funkcji w przedziale

Wartością największą lub najmniejszą w danym zbiorze nazywamy ekstremum globalnym.

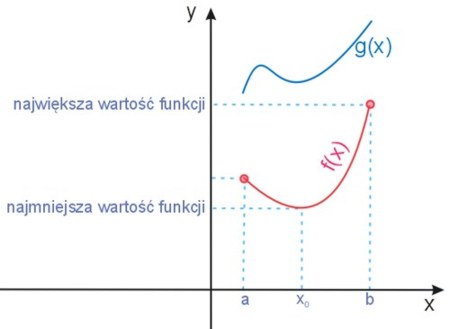
najwieksza i najmniejsza wartość funkcji w przedziale

Ilustracja przedstawia funkcję \(f(x)\) określoną w pewnym przedziale \(\langle a;b\rangle \).

Zaznaczono tutaj największą wartość funkcji (jest to wartość funkcji na krańcu przedziału) oraz najmniejszą (w tym przypadku jest to minimum). Kiedy jednak spojrzymy na funkcję \(g(x)\), to widać, że, mimo iż funkcja posiada minimum, to najmniejsza wartość funkcji będzie to wartość funkcji w początkowym punkcie przedziału. Funkcja posiada też maksimum, ale nie jest to największa wartość funkcji, gdyż jest nim wartość funkcji w końcu przedziału.

Aby wyznaczyć największą lub najmniejszą wartość funkcji w przedziale domkniętym \(\langle a;b\rangle \) należy:

Wyznaczyć ekstrema lokalne funkcji w tym przedziale.
Obliczyć wartości funkcji na końcach przedziału \(\langle a;b\rangle \), czyli \(f(a), f(b)\).
Wybrać najmniejszą i największą wartość z wyznaczonych wyżej liczb.

Pytania

Jak wyznaczyć ekstremum globalne w przedziale otwartym?

W takim przypadku, zamiast wartości funkcji na krańcach przedziału, obliczamy granice na krańcach przedziału, a jeśli się okaże, że wartość granicy jest największa lub najmniejsza, to funkcja nie przyjmuje wówczas któregoś ekstremum globalnego.