Asymptoty wykresu funkcji

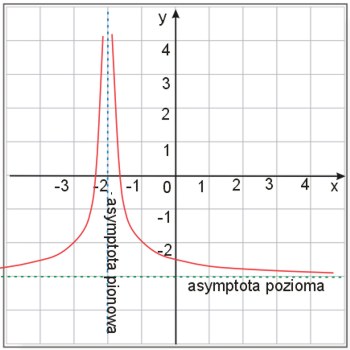
Asymptota jest to prosta, do której coraz bardziej „zbliża się” wykres pewnej funkcji. W dostatecznie odległych punktach krzywa prawie pokrywa się ze swoją asymptotą.

Rysunek przedstawia wykres, który posiada asymptotę tak zwaną pionową. Jest to prosta o równaniu \(x=-2\) zaznaczona przerywaną niebieską linią, ale posiada także asymptotę poziomą o równaniu \(y=-3\) (kolor zielony).

Pamiętać należy, że asymptoty nie są częścią wykresu, stanowią jedynie linie pomocnicze przy jego szkicowaniu.

Asymptota pozioma

Jeżeli funkcja \(f(x)\) jest określona w przedziale \((a;\infty)\) i istnieje granica \(\displaystyle\lim_{x\to +\infty}{f(x)}\), to prostą o równaniu \(y=b\) nazywamy asymptotą poziomą wykresu funkcji w plus nieskończoności.

Jeżeli funkcja \(f(x)\) jest określona w przedziale \((-\infty;a)\) i istnieje granica \(\displaystyle\lim_{x\to -\infty}{f(x)}\), to prostą o równaniu \(y=b\) nazywamy asymptotą poziomą wykresu funkcji w minus nieskończoności.

Jeśli asymptota pozioma w plus i minus nieskończoności ma to samo równanie, to nazywamy ją asymptotą obustronną.

Asymptota pionowa

Jeżeli funkcja \(f(x)\) jest określona w przedziale \((a;b)\) i \(\displaystyle\lim_{x\to a^+}{f(x)}=\pm \infty\), to prostą o równaniu \(x=a\) nazywamy prawostronną asymptotą pionową wykresu funkcji.

Jeżeli funkcja \(f(x)\) jest określona w przedziale \((a;b)\) i \(\displaystyle\lim_{x\to a^-}{f(x)}=\pm \infty\), to prostą o równaniu \(x=a\) nazywamy lewostronną asymptotą pionową wykresu funkcji.

Jeśli asymptota pozioma lewostronna i prawostronna opisana jest tym samym równaniem, to nazywamy ją asymptotą obustronną.

Asymptota ukośna (pochyła)

Wykres może również posiadać asymptotę ukośną prawostronną i lewostronną.

Jeżeli istnieją skończone granice:

\(\displaystyle\lim_{x\to +\infty}{\frac{f(x)}{x}}=a, \ \lim_{x\to +\infty}{[f(x)-ax]}=b\)

lub

\(\displaystyle\lim_{x\to -\infty}{\frac{f(x)}{x}}=a, \ \lim_{x\to -\infty}{[f(x)-ax]}=b\)

to prosta o równaniu \(y=ax+b\) jest asymptotą ukośną prawostronną w pierwszym i lewostronną w drugim przypadku.

Jeżeli powyższe granice nie istnieją, funkcja nie posiada asymptoty pochyłej.

Szczególnym przypadkiem jest \(a=0\). Wówczas asymptota ukośna staje się asymptotą poziomą.

Zadania z rozwiązaniami

Zadanie nr 1.

Znaleźć asymptoty funkcji \(f(x)=\frac{x^2-1}{4x^2}\).

Pokaż rozwiązanie zadania.

Zadanie nr 2.

Znaleźć asymptoty funkcji \(f(x)=\frac{x^2-3}{x-2}\).

Pokaż rozwiązanie zadania.

Powiązane materiały

Pochodna funkcji

Równanie stycznej do krzywej

Pochodna a monotoniczność funkcji

Pochodna funkcji a ekstremum

Największa i najmniejsza wartość funkcji

Test z zastosowania pochodnych