Pochodna a ekstremum funkcji

Pojęcie ekstremum zostało omówione w artykule Ekstremum funkcji. Tutaj zajmiemy się wykorzystaniem rachunku pochodnych do wyznaczania ekstremum funkcji. Opieramy się przy tym na następujących twierdzeniach:

Twierdzenie

Jeżeli funkcja f(x) ma ekstremum w punkcie x₀ i ma w tym punkcie pochodną, to .

Jest to warunek konieczny istnienia minimum lub maksimum funkcji. Twierdzenie odwrotne nie jest prawdziwe. Zobaczmy to na przykładzie:

Przykład

Dana jest funkcja , której wykres został przedstawiony obok. Przyjrzyjmy się punktowi x₀=0. Funkcja nie posiada w tym punkcie ani minimum, ani maksimum, natomiast gdy policzymy pochodną w tym punkcie:

$f'(x)=3x^2\\f'(0)=3\cdot{0^2}=0$

to widać, że przyjmuje ona wartość zero.

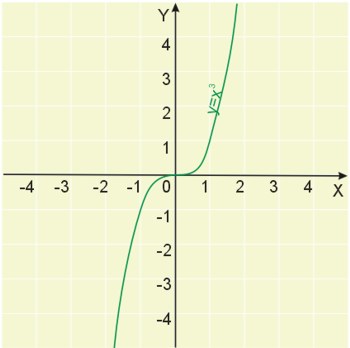
Zatem nie wystarczy sprawdzić, czy pochodna w danym punkcie posiada pochodną równą zeru, aby stwierdzić, że funkcja ma minimum lub maksimum.

Natomiast z całą pewnością, jeżeli pochodna w danym punkcie lub przedziale ma pochodną różną od zera, to nie ma w nim ekstremum.

Warunek wystarczający istnienia ekstremum
Jeżeli funkcja ma pochodną w pewnym otoczeniu punktu x₀, przy czym
1) dla $f'(x_0)>0 \ dla \ x<x_0 \ i \ f'(x_0)<0 \ dla \ x>x_0$ ,
to w punkcie x₀ funkcja posiada maksimum.
2) dla $f'(x_0)<0 \ dla \ x<x_0 \ i \ f'(x_0)>0 \ dla \ x>x_0$ ,
to w punkcie x₀ funkcja posiada minimum.

Mówiąc krótko:

Jeżeli pochodna przy przejściu zmiennej x przez punkt x₀ zmienia znak z ujemnego na dodatni, to funkcja f(x) osiąga minimum w tym punkcie.

Jeżeli pochodna przy przejściu zmiennej x przez punkt x₀ zmienia znak z dodatniego na ujemny, to funkcja f(x) osiąga maksimum w tym punkcie.

Zobaczmy to na przykładzie:

Przykład

Dana jest funkcja , której wykres został przedstawiony obok. (Sam możesz sporządzić wykres tej funkcji, korzystając z tej symulacji)

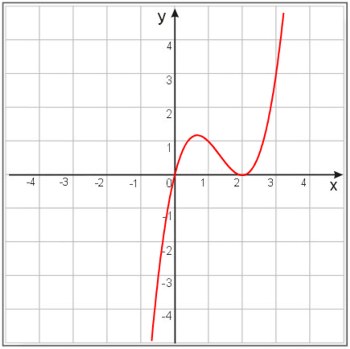
Znajdziemy ekstrema tej funkcji, obliczając pochodną funkcji:

Ekstremum szukamy w punktach, gdzie pochodna przyjmuje wartość zero. Mamy więc:

$3x^2-8x+4=0 \\ \Delta=b^2-4ac=64-4\cdot 3\cdot 4=64-48=16\\ x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{8-4}{6}=\frac{2}{3}\\ x_2=\frac{-b+\sqrt{\Delta}}{2a}=\frac{8+4}{6}=2\\ 3(x-\frac{2}{3})(x-2)=0$

Funkcja f(x) może mieć ekstremum tylko w punktach 2/3 i 2

Warto sporządzić tabelkę zmienności pochodnej funkcji:

Gdy sporządzimy wykres:

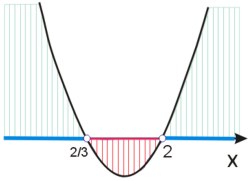
to widzimy, gdzie pochodna przyjmuje dodatnie wartości (kolor niebieski), a gdzie ujemne (kolor różowy).

$(-\infty;\frac{2}{3})$	$\frac{2}{3}$	$(\frac{2}{3},2)$		$(2;\infty)$
+	0	-	0	+

W punkcie 2/3 funkcja ma więc maksimum, w punkcie 2 - minimum. Musimy je jeszcze obliczyć. Wystarczy policzyć wartość funkcji w tych punktach:

$f(\frac{2}{3})=(\frac{2}{3})^3-4\cdot(\frac{2}{3})^2+4\cdot \frac{2}{3}=\frac{8}{27}-4\cdot \frac{4}{9}+\frac{8}{3}=\frac{8}{27}-\frac{48}{27}+\frac{72}{27}=\frac{32}{27}=1\frac{5}{27}$
$f(2)=2^3-4\cdot 2^2+4\cdot 3=8-16+8=0$

Zadania z rozwiązaniami

Zadania związane z tematem:
Pochodna funkcji a ekstremum

Zadanie - badanie ekstremum funckji
Znaleźć ekstremum funkcji $f(x)=\sqrt{1-x^2}$ .

Pokaż rozwiązanie zadania

Zadanie - ekstremum funkcji i pochodna
Znaleźć ekstremum funkcji $f(x)=2x-\frac{1}{x}$ .

Pokaż rozwiązanie zadania

Zadanie - ekstremum funkcji a pochodna
Znaleźć ekstremum funkcji $f(x)=2x+\frac{1}{x}$ .

Pokaż rozwiązanie zadania

Zadanie - ekstremum funkcji i pochodna
Znaleźć ekstremum funkcji $f(x)=\frac{2x}{x^2+1}$ .

Pokaż rozwiązanie zadania

Zadanie - największa i najmniejsza wartośćfunkcji
Znaleźć największą i najmniejszą wartość funkcji $f(x)=3x+\frac{1}{x}$ w przedziale <-1;1>.

Pokaż rozwiązanie zadania

Zadanie maturalne nr 16, matura 2016 (poziom rozszerzony)
Parabola o równaniu $y=2-\frac{1}{2}x^2$ przecina oś Ox układu współrzędnych w punktach A = (- 2,0) i B = (2,0). Rozpatrujemy wszystkie trapezy równoramienne ABCD, których dłuższą podstawą jest odcinek AB, a końce C i D krótszej podstawy leżą na paraboli (zobacz rysunek).
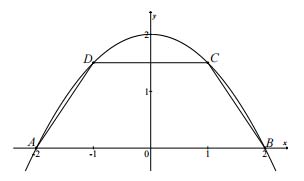
Zadanie 16, ilustracja, matura 2016
Wyznacz pole trapezu ABCD w zależności od pierwszej współrzędnej wierzchołka C. Oblicz współrzędne wierzchołka C tego z rozpatrywanych trapezów, którego pole jest największe.

Pokaż rozwiązanie zadania

Inne zagadnienia z tej lekcji

Równanie stycznej do krzywej
Styczna do krzywej y=f(x) w punkcie A(x0,f(x0)) określona jest równaniem: y-y_0=f'(x_0)(x-x_0)

Pochodna a monotoniczność funkcji
Aby sprawdzić czy funkcja jest rosnąca czy malejąca w danym przedziale należy zbadać znak pochodnej.

Największa i najmniejsza wartość funkcji
Jak wyznaczyć ekstremum globalne w przedziale otwartym?

Pochodna w zadaniach z treścią
Zastosowanie pochodnej w zadaniach z treścią

Test wiedzy
Sprawdź swoje umiejętności z materiału zawartego w tej lekcji.