Ciągłość funkcji

Ciągłość funkcji możemy rozpatrywać w danym punkcie lub w przedziale argumentów funkcji. Omówimy oba przypadki.

Ciągłość funkcji w punkcie

Definicja ciągłości funkcji w punkcie jest następująca:

Zakładamy, że funkcja \(f(x)\) jest określona w otoczeniu punktu \(x_0\).

Definicja

Mówimy, że funkcja \(f(x)\) jest ciągła w punkcie \(x_0\), jeżeli:

\(\displaystyle\lim_{x\to x_0}{f(x)}=f(x_0)\)

Zatem funkcja \(f(x)\) jest ciągła w punkcie \(x_0\), jeżeli:

ma w punkcie \(x_0\) granicę równą \(g\),
posiada w punkcie \(x_0\) wartość \(f(x_0)\),
granica \(g\) równa jest wartości funkcji \(f(x_0)\).

Przykład

Zbadać ciągłość funkcji \(f(x)=\begin{cases}3\ dla\ x\geq 1\\x \ dla \ x<1\end{cases}\) w punkcie \(x_0=1\).

W tym celu obliczamy granicę lewostronną i prawostronną i lewostronną:

\(\lim_{x\to 1+}{f(x)}=\lim_{x\to 1+}{3}=3\)

\(\lim_{x\to 1-}{f(x)}=\lim_{x\to 1-}{x}=1\)

Ponieważ w punkcie \(x_0=1\) granice prawostronna i lewostronna nie są sobie równe, to nie istnieje granica w tym punkcie, a funkcja nie jest ciągła w tym punkcie.

Warto jeszcze przyjrzeć się wykresowi tej funkcji, aby móc sobie wyobrazić, na czym polega ciągłość lub brak ciągłości funkcji w punkcie.

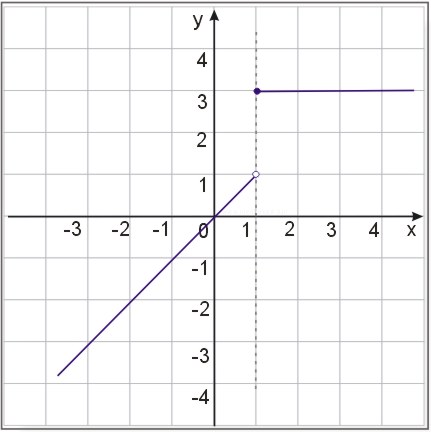
Wykres - ciągłość

Zauważ, że w każdym innym punkcie funkcja ta jest ciągła.

Jeżeli w danym punkcie funkcja posiada granicę tylko jednostronną, to mówimy o ciągłości jednostronnej (prawostronnej lub lewostronnej).

Ciągłość funkcji w przedziale

Definicja

Funkcja \(f(x)\) jest ciągła w przedziale otwartym \((a;b)\), wtedy i tylko wtedy, gdy jest ciągła w każdym punkcie tego przedziału.

Definicja

Funkcja \(f(x)\) jest ciągła w przedziale domkniętym \(\langle a;b \rangle\), wtedy i tylko wtedy, gdy jest ciągła w przedziale \((a;b)\) oraz jest prawostronnie ciągła w punkcie \(x_0=a\) i lewostronnie ciągła w punkcie \(x_0=b\).

Ciągłość funkcji elementarnych

Twierdzenie o ciągłości funkcji elementarnych.

Wszystkie funkcje elementarne (wielomiany, funkcje wymierne, wykładnicze, logarytmiczne, trygonometryczne) są ciągłe w swoich dziedzinach.

Poniższa ilustracja pokazuje dwie różne funkcje. Jedna z nich jest ciągła, druga nie.

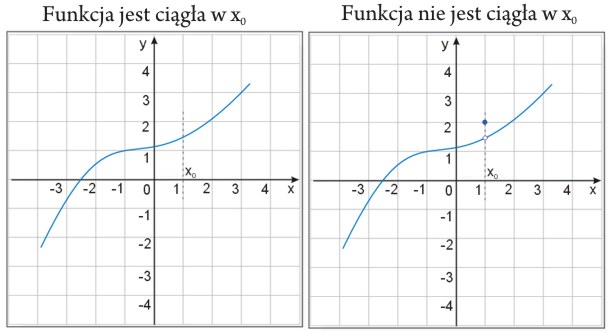
przykłady ciągłości funkcji

Badanie ciągłości funkcji

Badanie ciągłości funkcji możemy przeprowadzać na podstawie badania granic funkcji tak, jak to pokazano na powyższym przykładzie. Częściej jednak badanie ciągłości odbywa się z wykorzystaniem pojęcia pochodnej funkcji. Między ciągłością funkcji a istnieniem pochodnej funkcji w danym punkcie istnieje silna zależność. Omawiamy ją w artykule: Różniczkowalność a ciągłość funkcji.

Zadania z rozwiązaniami

Zadanie nr 1.

Zbadać, czy funkcja \(f(x)=\begin{cases} -2x, \ dla \ x \leq 0 \\ x^2, \ dla \ x > 0 \end{cases}\) jest ciągła w punkcie \(x_0=0\).

Pokaż rozwiązanie zadania.

Zadanie nr 2.

Dla jakich wartości parametru \(a\) funkcja \(f(x)=\begin{cases} 2x^2-a, \ dla \ x \geq 1 \\ x-1, \ dla \ x < 1 \end{cases}\) jest ciągła w punkcie \(x_0=1\)?

Pokaż rozwiązanie zadania.

Zadanie nr 3.

Sprawdzić, czy funkcja \(f(x)=\begin{cases} \frac{x^2+x-6}{x-2}, \ dla \ x\in(-\infty;2) \\5, \ dla\ x=2 \\ 3x-1, \ dla \ x\in (2;\infty) \end{cases}\) jest ciągła w zbiorze liczb rzeczywistych.

Pokaż rozwiązanie zadania.

Zadanie nr 4.

Sprawdzić, czy funkcja \(f(x)=|x+1|-x\) jest ciągła w punkcie \(x_0=-1\).

Pokaż rozwiązanie zadania.

Powiązane materiały

Granica funkcji

Pochodna funkcji