Wielomian
Co to jest wielomian jednej i wielu zmiennych? Jakie zastosowania mają wielomiany?
Definicja
Wielomianem jednej zmiennej rzeczywistej \(x\) nazywamy funkcję:
gdzie:
- \(n\) — jest to tak zwany stopień wielomianu, \(n\in \mathbb{N}_0\),
- \(a_0, a_1, a_2, ..., a_n\) — liczby dane rzeczywiste, tak zwane współczynniki wielomianu,
- \(a_0\) — wyraz wolny wielomianu.
W zależności od liczby wyrazów w wielomianie będziemy go nazywać jednomianem, dwumianem, trójmianem itd.
Stopień wielomianu
Stopień wielomianu to największa potęga, w jakiej występuje zmienna wielomianu.
Jednomian
Jednomian jest to wyrażenie algebraiczne w postaci \(ax^n\), gdzie \(a\in \mathbb{R}\).
Dwumian
Dwumian jest to wyrażenie algebraiczne będące sumą dwóch jednomianów.
Trójmian
Trójmian jest to wyrażenie algebraiczne będące sumą trzech jednomianów.
Przykłady wielomianów
Oto kilka przykładów wielomianów wraz z ich opisem.
| Wielomian | Nazwa wielomianu | Stopień wielomianu | Wyjaśnienia |
|---|---|---|---|
| \(y=5x^2+3x-1\) | Trójmian | 2 | Ponieważ wielomian ma 3 wyrazy, nazywamy go trójmianem. |
| \(y=5x-x^5\) | Dwumian | 5 | Kolejność wyrazów nie ma znaczenia przy określaniu stopnia wielomianu. |
| \(y=2+x-x^2+3x^3-x^4\) | Pięciomian | 4 | — |
| \(y=5x\) | Jednomian | 1 | — |
| \(y=1\) | Jednomian | 0 | — |
| \(y=0\) | Jednomian zerowy | Nie określa się stopnia jednomianu zerowego. | Dla \(n=0\) jednomian jest w postaci \(y=ax^0\) i dla \(x=0\) nie jest określony. Rozszerzamy dziedzinę takiego wielomianu tak, że dla \(x=0\) wielomian przyjmuje wartość \(y=a\). |
Wielomiany oznaczamy dużymi literami, podając w nawiasie oznaczenie zmiennej: \(W(x), A(y), B(z)\) itd.
Wielomian jest sumą jednomianów. Jeżeli dwa jednomiany tej samej zmiennej są tego samego stopnia, to mówimy, że są podobne. Jednomiany podobne można redukować, zastępując ich sumę jednym wielomianem, a wielomian, którego wyrazy są ułożone od najwyższego stopnia do najniższego i który nie zawiera jednomianów podobnych, nazywamy wielomianem uporządkowanym i zredukowanym.
Przykłady
Wielomian \(W(x)=x^2-1+3x^2\) nie jest uporządkowany ani zredukowany. Zredukujemy go, dodając do siebie wyrazy \(x^2+3x^2=4x^2\) i porządkując wyrazy od najwyższej potęgi: \(W(x)=4x^2-1\). Teraz widać, że jest to dwumian stopnia drugiego.
Działania na wielomianach
W osobnych artykułach omawiamy działania na wielomianach:
Pytania
Jak wykazać równość wielomianów?
Kiedy wielomiany są równe? Równość wielomianów wykazujemy poprzez porównanie wszystkich współczynników tych wielomianów. Zasadę tę wykorzystuje się między innymi przy rozwiązywaniu zadań z wielomianami z parametrem. Na przykład wielomian \(ax-1\) jest równy wielomianowi \(2x+b\), jeżeli \(a=2\) i \(b=-1\).
Jak odczytać stopień i współczynniki wielomianu?
Stopień wielomianu odczytujemy wprost ze wzoru wielomianu, gdy tylko ten występuje jako suma jednomianów. Stopień wielomianu jest to wówczas największa potęga, w jakiej występuje zmienna. Jeżeli jednak wielomian występuje w innej postaci, na przykład iloczynowej, wtedy najlepiej wykonać działania na wielomianach i doprowadzić do postaci sumy jednomianów. Wtedy bez trudu otrzymamy współczynniki wielomianu oraz jego stopień.
Aby określić stopień wielomianu, który ma postać iloczynu innych wielomianów, możemy się domyślać stopnia wielomianu po tym, ile razy zmienna zostanie pomnożona przez samą siebie. Na przykład wielomian \(W(x)=(x-2)(x+5)\) jest wielomianem kwadratowym, a wielomian \(G(x)=(x^2-4)^2(x-1)\) jest wielomianem stopnia piątego (najwyższą — drugą potęgę niewiadomej podnosimy do kwadratu i mamy tu jeszcze iloczyn zmiennej, będącej w pierwszej potędze).
Zadania z rozwiązaniami

Zadanie nr 1.
Dany jest wielomian: \(A(x)=x^3-x^2+x-1\). Obliczyć \(A(-1), \ A(2),\ A(\sqrt{2}), A(-\sqrt[3]{2})\).
Powiązane materiały
© medianauka.pl, 2009-08-17, A-280
Data aktualizacji artykułu: 2023-04-23

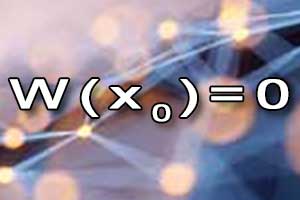 Pierwiastki wielomianu — twierdzenie Bezouta
Pierwiastki wielomianu — twierdzenie Bezouta Wykres wielomianu
Wykres wielomianu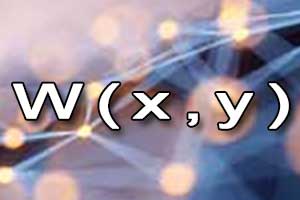 Wielomian dwóch zmiennych
Wielomian dwóch zmiennych Wielomian
Wielomian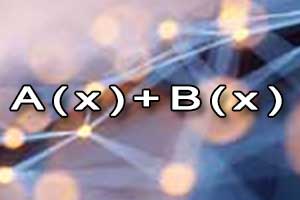 Dodawanie i odejmowanie wielomianów
Dodawanie i odejmowanie wielomianów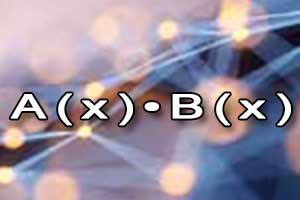 Mnożenie wielomianów
Mnożenie wielomianów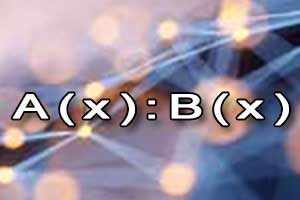 Dzielenie wielomianów
Dzielenie wielomianów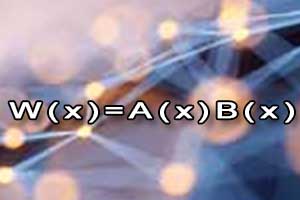 Rozkład wielomianu na czynniki
Rozkład wielomianu na czynniki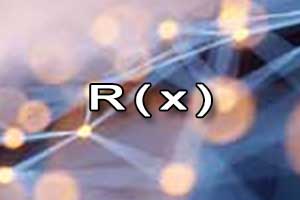 Schemat Hornera
Schemat Hornera