Wykres wielomianu

Sporządzenie wykresu funkcji wielomianowej wymaga przeprowadzenie analizy funkcji i nie jest łatwe. Badanie funkcji będzie omawiane przy okazji zastosowania pochodnej. Teraz za pomocą symulacji możesz prześledzić przebieg funkcji wielomianowej, aby mieć wyobrażenie o tym zagadnieniu.

Wykres

Wykres wielomianu online

Funkcja w postaci y = ax⁶+bx⁵+cx⁴+dx³+ex²+fx+g, czyli y = x

a 1 b 0

c 0 d 0

e 0 f 0

g 0

WYKRESY ONLINE

Narysuj wykres funkcji w programie do szkicowania wykresów i odczytaj jego własności.

Rysowanie wykresu wielomianu

Umiejętność szybkiego sporządzania wykresu wielomianu przydaje się przy rozwiązywaniu równań i nierówności wielomianowych. Rysowanie sprowadza się wówczas do zwykłego szkicu, skupiając się jedynie na miejscach zerowych funkcji oraz na znaku funkcji w poszczególnych przedziałach wyznaczonych przez te miejsca zerowe. Sam przebieg funkcji nie jest w tym przypadku ważny.

Jak narysować wykres wielomianu? Zasada sporządzania szkicu przebiegu funkcji jest następująca:

Przedstawiamy funkcję w postaci iloczynowej: \(f(x)=a(x-x_1)^{p_1}(x-x_2)^{p_2}...(x-x_n)^{p_n}R(x)\).
Zaznaczamy wszystkie miejsca zerowe na osi OX.
Jeżeli \(a>0\), to zaczynając od prawej strony, rysujemy krzywą od góry w kierunku ostatniego miejsca zerowego i przeciągamy krzywą do kolejnych miejsc zerowych, przecinając oś OX tylko wtedy, gdy potęga \(p\) jest nieparzysta.
Jeżeli \(a<0\), to zaczynając od prawej strony, rysujemy krzywą od dołu w kierunku ostatniego miejsca zerowego i przeciągamy krzywą do kolejnych miejsc zerowych, przecinając oś OX tylko wtedy, gdy potęga p jest nieparzysta.

Przykład

Naszkicować przebieg funkcji \(f(x)=5x^2(x-1)^3(x+1)\).

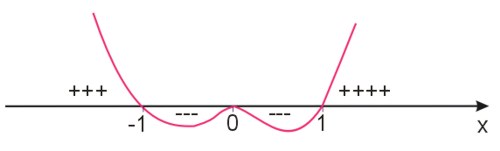
Zgodnie z powyższymi zasadami współczynnik \(a\) jest dodatni, więc zaczynamy rysować wykres od góry. Zbliżamy się do pierwszego miejsca zerowego równego 1. Mamy tu do czynienia z nieparzystą potęgą (trzecią), więc przechodzimy z wykresem na drugą stronę osi. Potem docieramy do drugiego miejsca zerowego, równego zeru. Tutaj mamy czynnik \(x\) w drugiej, czyli parzystej potędze, zatem nie przechodzimy na drugą stronę wykresu, a odbijamy się od niej. Następnie kierujemy się do ostatniego miejsca zerowego. Czynnik ten jest w pierwszej, czyli nieparzystej potędze, więc przechodzimy z wykresem na drugą stronę.

Mamy szkic funkcji.

Aby zobaczyć jak wygląda wykres tej funkcji, skorzystaj z powyższej aplikacji. Musisz najpierw jednak wyrazić wielomian w postaci sumy jednomianów (trzeba wykonać działania).

\(f(x)=5x^2(x-1)^3(x+1)=5x^6-10x^5+10x^3-5x^2\)

Ustaw więc odpowiednie współczynniki a, b, c, d, e, f na 5, -10, 0, 10, -5, 0, 0 (zaznacz suwak i używaj strzałek) i zobacz efekt.