Dzielenie wielomianów
Wielomiany możemy dzielić przez siebie. Iloraz wielomianów dość często pojawia się w kursie matematyki przy okazji rozwiązywania równań i nierówności wielomianowych. Dzielnik wielomianu nie może być wielomianem zerowym, a stopień wielomianu będącym ilorazem jest co najwyżej równy stopniowi niezerowej dzielnej.
Przykłady
Dzielenie pisemne wielomianów wymaga nieco wprawy. Warto więc rozwiązać kilka przykładów. Najczęściej wykonuje się dzielenie pisemne wielomianów przez dwumian.
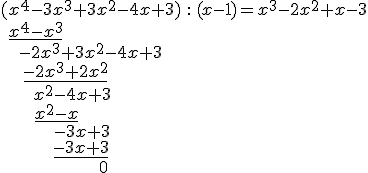
Reszta z dzielenia wielomianu
Twierdzenie o rozkładzie wielomianu
Jeżeli \(W(x), P(x)\) są wielomianami i \(P(x)\) nie jest wielomianem zerowym, to istnieją takie wielomiany \(Q(x), R(x)\), że \(W(x)=Q(x)P(x)+R(x)\).
Wielomian \(R(x)\) może być wielomianem zerowym albo jego stopień jest mniejszy od stopnia wielomianu \(P(x)\).
Przykłady
Poniższy przykład ilustruje dzielenie wielomianów z resztą:
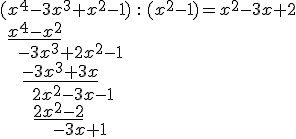
Otrzymaliśmy resztę z dzielenia i możemy zapisać powyższe działanie zgodnie z przytoczonym twierdzeniem:
\((x^4-3x^3+x^2-1)=(x^2-3x+2)(x^2-1)+(-3x+1)\)
gdzie \((-3x+1)\) jest resztą z dzielenia.
Jednak najczęściej wynik zapisujemy w następujący sposób:
\((x^4-3x^3+x^2-1):(x^2-1)=x^2-3x+2+\frac{-3x+1}{x^2-1}\)
Twierdzenie o reszcie z dzielenia wielomianu przez dwumian
Reszta dzielenia wielomianu \(W(x)\) przez \((x−a)\) jest równa wartości tego wielomianu w punkcie \(a\), tzn. \(W(a)\).
Zadania z rozwiązaniami

Zadanie nr 1.
Dla jakiej wartości parametru a wielomian \(W(x)=x^3+2x^2-x+a\) dzieli się bez reszty przez \(x-1\)?

Zadanie nr 2.
Wykonać dzielenie wielomianów:
a) \((x^5+x^2-x+1):(x^3-x+1)\)
b) \((8x^4-2x^3-5x^2-13x-3):(x^2+x+1)\)
c) \((x^{10}-1):(x^2+1)\)
d) \((8x^3+18x^2-9x-8):(x+\frac{1}{2})\)
e) \((x^4-2\sqrt{2}x^3-2x^2+8\sqrt{2}x-8):(x-\sqrt{2})\)

Zadanie nr 3 — maturalne.
Wielomian \(W(x)=6x^3+3x^2-5x+p\) jest podzielny przez dwumian \(x-1\) dla \(p\) równego:
A. \(4\)
B. \(-2\)
C. \(2\)
D. \(-4\)

Zadanie nr 4 — maturalne.
Dany jest wielomian \(W(x)=2x^3+ax^2−13x+b\). Liczba 3 jest jednym z pierwiastków tego wielomianu. Reszta z dzielenia wielomianu \(W(x)\) przez (x+2) jest równa 20. Oblicz współczynniki \(a\) i \(b\) oraz pozostałe pierwiastki wielomianu \(W(x)\).
Powiązane materiały
© medianauka.pl, 2009-08-18, A-284
Data aktualizacji artykułu: 2023-04-25

 Wielomian
Wielomian Pierwiastki wielomianu — twierdzenie Bezouta
Pierwiastki wielomianu — twierdzenie Bezouta Wykres wielomianu
Wykres wielomianu Wielomian dwóch zmiennych
Wielomian dwóch zmiennych Wielomian
Wielomian Dodawanie i odejmowanie wielomianów
Dodawanie i odejmowanie wielomianów Mnożenie wielomianów
Mnożenie wielomianów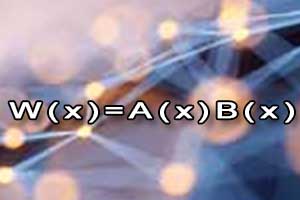 Rozkład wielomianu na czynniki
Rozkład wielomianu na czynniki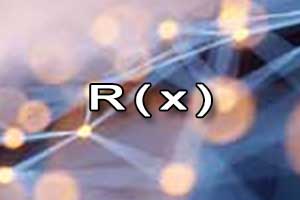 Schemat Hornera
Schemat Hornera