Funkcja kwadratowa

Funkcję w postaci

$y=ax^2+bx+c$

gdzie $x\in{R},\quad{a}\in \mathbb{R}\setminus \lbrace 0 \rbrace, b, c\in \mathbb{R}$, nazywamy funkcją kwadratową, trójmianem kwadratowym (gdy $b\neq 0, c\neq 0$) lub funkcją drugiego stopnia.

Przedstawiony wyżej wzór funkcji kwadratowej jest to tak zwana postać ogólna funkcji kwadratowej.

W dalszej części kursu poznamy:

postać iloczynową funkcji kwadratowej,
postać kanoniczną funkcji kwadratowej.

Przykłady

Przykłady funkcji kwadratowych w postaci ogólnej:

$y=5x^2+9x-4$
${y=-x^2-x}$
${y=2x^2-7}$
${y=x^2}$

A oto inne przykłady funkcji kwadratowej w innej postaci:

$y=(x-1)(x+1)$
$y=x(x+4)$
$y=3(x-\frac{1}{2})(x+\frac{1}{2})$
$y=5(x-1)^2+6$

Jednomian kwadratowy

Szczególnym przypadkiem trójmianu kwadratowego jest jednomian drugiego stopnia (kwadratowy).
Jest to funkcja w postaci $y=ax^2$. Jest to więc przypadek, w którym $b=c=0$.

Funkcja kwadratowa — wzory

Oto przydatne wzory i zagadnienia związane z funkcją kwadratową oraz linki do artykułów, w których wzory te zostały omówione. Jednocześnie prezentujemy różne postacie funkcji kwadratowej.

Zagadnienie	Wzór
Postać ogólna funkcji kwadratowej	$y=ax^2+bx+c$
Postać iloczynowa funkcji kwadratowej	Postać iloczynowa: $y=a(x-x_1)(x-x_2)$ Pierwiastki funkcji kwadratowej (miejsca zerowe funkcji kwadratowej): $x_1=\frac{-b-\sqrt{\Delta}}{2a},\quad{x_2=\frac{-b+\sqrt{\Delta}}{2a}}$ Wyróżnik trójmianu kwadratowego: $\Delta=b^2-4ac$ Miejsce zerowe funkcji kwadratowej, gdy $\Delta=0$: $x_0=-\frac{b}{2a}$
Postać kanoniczna trójmianu kwadratowego	Postać kanoniczna: $y=a(x+\frac{b}{2a})^2-\frac{\Delta}{4a}$ Wektor przesunięcia: $\vec{u}=[-\frac{b}{2a},-\frac{\Delta}{4a}]$ Współrzędne wierzchołka paraboli: $W(-\frac{b}{2a},-\frac{\Delta}{4a})$
Wzory Viete'a	$x_1+x_2=-\frac{b}{a}$ $x_1\cdot{x_2}=\frac{c}{a}$

Wykresfunkcji kwadratowej

Wykresem funkcji kwadratowej jest parabola.

Wykres trójmianu kwadratowego będziemy sporządzać korzystając z możliwości przesuwania wykresu jednomianu kwadratowego o określony wektor w układzie współrzędnych. Będziemy to omawiać przy okazji postaci kanonicznej trójmianu kwadratowego. Poznajmy cechy paraboli w oparciu o jednomian kwadratowy.

Przykłady

Sporządźmy wykresy kilku funkcji:

$y=x^2$,

$y=-x^2$,

$y=2x^2$ ,

$y=\frac{1}{2}x^2$,

gdzie $a$ jest dowolną liczbą.

Sporządźmy tabelkę zmienności funkcji.

$x$	-2	-1	$\frac{1}{2}$	1	2
$y=x^2$	4	1	$\frac{1}{4}$	1	4
$y=-x^2$	-4	-1	$-\frac{1}{4}$	-1	-4
$y=2x^2$	8	2	$\frac{1}{2}$	2	8
$y=\frac{1}{2}x^2$	2	$\frac{1}{2}$	$\frac{1}{8}$	$\frac{1}{2}$	2

Na jednym układzie współrzędnych wykreślamy wykresy wszystkich funkcji.

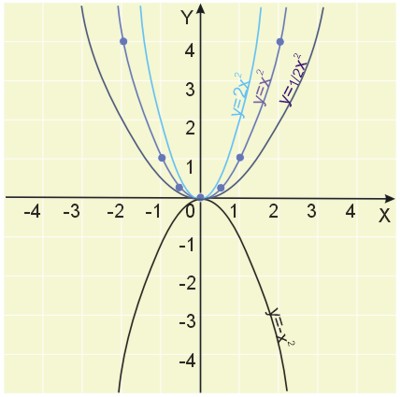
Wykres jednomianu kwadratowego

Własności funkcji kwadratowej na przykładzie jednomianu kwadratowego

Podstawowe własności funkcji kwadratowej można określić na podstawie przykładu jednomianu kwadratowego.

Wykresem jednomianu kwadratowego jest krzywa, którą nazywamy parabolą.
Parabola ma dwa ramiona, które mogą być skierowane w górę, gdy współczynnik $a>0$ oraz skierowane w dół, kiedy współczynnik $a<0$.
Im większy jest współczynnik $a$, tym parabola jest „węższa”.
Parabola (o równaniu $y=ax^2$) posiada jeden wierzchołek w punkcie $W=(0,0)$.
Parabola jednomianu kwadratowego ma oś symetrii. Jest to prosta o równaniu $x=0$.
Dziedzina funkcji kwadratowej: dziedziną funkcji kwadratowej jest zbiór liczb rzeczywistych.
Zbiór wartości funkcji kwadratowej: zbiorem wartości jednomianu kwadratowego jest zbiór $\langle 0;+\infty)$, gdy $a>0$ oraz $(-\infty;0 \rangle$, gdy $a<0$.
Jednomian kwadratowy jest funkcją parzystą. Oś OY jest osią symetrii paraboli, a punkt przecięcia się tej osi z parabolą jest wierzchołkiem paraboli.
Monotoniczność jednomianu kwadratowego: funkcja maleje w przedziale $(-\infty;0)$ i rośnie w przedziale $(0;+\infty)$, gdy $a>0$ oraz rośnie w przedziale $(-\infty;0)$ i maleje w przedziale $(0;+\infty)$, gdy $a<0$.
Największa i najmniejsza wartość funkcji kwadratowej. Gdy $a<0$ funkcja osiąga wartość największą (maksimum) w punkcie $x=0$ równe $0$, natomiast dla $a>0$ funkcja osiąga wartość najmniejszą (minimum) w punkcie $x=0$ równe $0$.
Jednomian kwadratowy ma jedno miejsce zerowe $x_0=0$.

Własności dowolnej funkcji kwadratowej zostały omówione w artykule o wykresie funkcji kwadratowej (link na końcu artykułu).

W artykule tym zbadasz też zmienność wykresu funkcji kwadratowej w zależności od współczynników $a, b, c$ dzięki aplikacji tam udostępnionej. Można tutaj za pomocą suwaków zmieniać wartości odpowiednich współczynników i obserwować zachowanie wykresu funkcji kwadratowej.

Pytania

Czy funkcja kwadratowa i trójmian kwadratowy to jest to samo?

Jest pewna różnica między funkcją kwadratową a trójmianem kwadratowym. Nie każda funkcja kwadratowa jest trójmianem, ale każdy trójmian kwadratowy jest funkcją kwadratową. Istnieją dwumiany i jednomiany, które są funkcjami kwadratowymi (np. $y=5x^2-3x, y=2x^2$). Gdy $a$, $b$ i $c$ są różne od zera, wówczas funkcja kwadratowa jest trójmianem kwadratowym.

Ćwiczenia

Ćwiczenia interakcyjne pomogą przygotować się na sprawdzian, test, egzamin, a ponadto usystematyzują wiedzę z danej dziedziny. To także świetny trening do matury. Wiele ćwiczeń to dobre zadania maturalne.

ĆWICZENIA

Funkcja kwadratowa

Zadania z rozwiązaniami

Zadanie nr 1 — maturalne.

Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej f. Wierzchołkiem tej paraboli jest punkt W = (1,9). Liczby -2 i 4 to miejsca zerowe funkcji f.

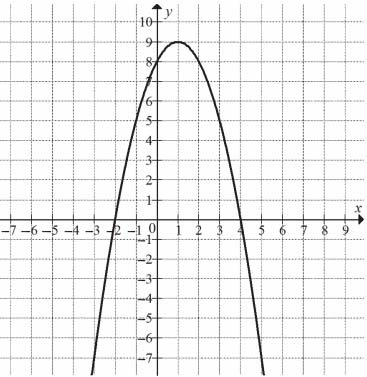
ilustracja do zadania nr 10 matura 2016

Zbiorem wartości funkcji f jest przedział:

A. (-∞,-2>

B. <-2,4>

C. <4,∞)

Pokaż rozwiązanie zadania.

Zadanie nr 2 — maturalne.

Funkcja kwadratowa określona jest wzorem f(x) = x²+x+c. Jeżeli f(3) = 4, to:

A. f(1) = -6

B. f(1) = 0

C. f(1) = 6

D. f(1) = 18

Pokaż rozwiązanie zadania.

Zadanie nr 3 — maturalne.

Oblicz najmniejszą i największą wartość funkcji kwadratowej f(x) = x²-6x + 3 w przedziale <0,4>.

Pokaż rozwiązanie zadania.

Zadanie nr 4 — maturalne.

Liczby (-1) i 3 są miejscami zerowymi funkcji kwadratowej f. Oblicz $\frac{f(6)}{f(12)}$ .

Pokaż rozwiązanie zadania.

Zadanie nr 5 — maturalne.

Na rysunku przedstawiono fragment wykresu funkcji kwadratowej $f(x)=ax^2+bx +c$, której miejsca zerowe to: −3 i 1.

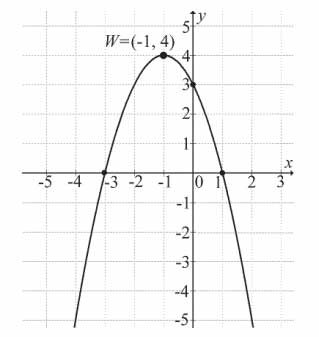
Rysunek do zadania

Współczynnik c we wzorze funkcji f jest równy:

A. 1

B. 2

C. 3

D. 4

Pokaż rozwiązanie zadania.

Zadanie nr 6.

Piąty wyraz ciągu geometrycznego jest równy $\frac{1}{\sqrt{2}}$, a siódmy $\sqrt{2}$. Znaleźć dziewiąty wyraz ciągu i obliczyć sumę pierwszych dziesięciu wyrazów tego ciągu geometrycznego.

Pokaż rozwiązanie zadania.

Inne zagadnienia z tej lekcji

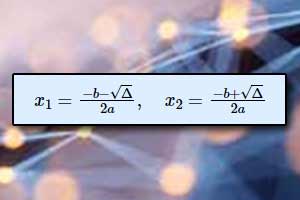Miejsca zerowe funkcji kwadratowej

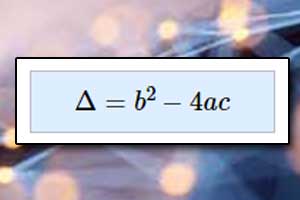Postać kanoniczna funkcji kwadratowej

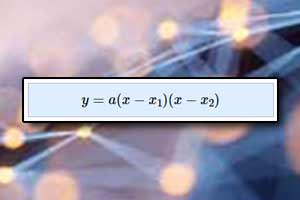Postać iloczynowa trójmianu kwadratowego

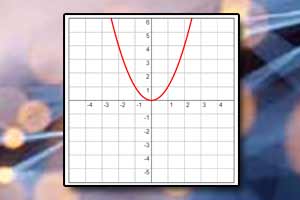Parabola

Właściwości i wykres funkcji kwadratowej

\(x\)	-2	-1	\(\frac{1}{2}\)	1	2
\(y=x^2\)	4	1	\(\frac{1}{4}\)	1	4
\(y=-x^2\)	-4	-1	\(-\frac{1}{4}\)	-1	-4
\(y=2x^2\)	8	2	\(\frac{1}{2}\)	2	8
\(y=\frac{1}{2}x^2\)	2	\(\frac{1}{2}\)	\(\frac{1}{8}\)	\(\frac{1}{2}\)	2