Wzory Viete'a
Jeżeli równanie kwadratowe ma pierwiastki, to prawdziwe są wzory Viete'a (czytaj: wzory Vieta):
\(x_1+x_2=-\frac{b}{a}\)
\(x_1\cdot{x_2}=\frac{c}{a}\)
Jeżeli równanie kwadratowe ma jeden podwójny pierwiastek, to wzory Viete'a przyjmują postać:
\(2x_0=-\frac{b}{a}\)
\({x_0}^2=\frac{c}{a}\)
Wyprowadzenie wzorów Viete'a
Aby dowieść prawdziwości wzorów Viete'a wystarczy obliczyć sumę pierwiastków równania kwadratowego oraz iloczyn pierwiastków równania kwadratowego.
\(x_1+x_2=\frac{-b-\sqrt{\Delta}}{2a}+\frac{-b+\sqrt{\Delta}}{2a}=\frac{-b-\sqrt{\Delta}-b+\sqrt{\Delta}}{2a}=\frac{-2b}{2a}=-\frac{b}{a}\)
\(x_1\cdot{x_2}=\frac{-b-\sqrt{\Delta}}{2a}\cdot{\frac{-b+\sqrt{\Delta}}{2a}}=\frac{(-b)^2-(\sqrt{\Delta})^2}{(2a)^2}=\frac{b^2-(b^2-4ac)}{4a^2}=\frac{4ac}{4a^2}=\frac{c}{a}\)
Zastosowanie wzorów Viete'a
Wzory Viete'a są pomocne przy układaniu równań kwadratowych lub wówczas, gdy mamy pewną wiedzę na temat pierwiastków równania. Poniżej przykład takiego zadania.
Przykłady
Znaleźć dowolne równanie kwadratowe, którego suma pierwiastków jest równa 4, a iloczyn jest równy 2.
Korzystając ze wzorów Viete'a mamy:
\(4=-\frac{b}{a}\quad{i}\quad{2}=\frac{c}{a}\)
\(b=-4a\quad{i}\quad{c}=2a\)
Zatem równanie kwadratowe będzie miało postać:
\(ax^2+bx+c=0\)
\(ax^2-4ax+2a\)
Parametr \(a\) może być dowolną liczbą różną od zera. Ponieważ mamy znaleźć dowolne równanie kwadratowe, możemy przyjąć dowolną wartość \(a\). Jeżeli założymy, że \(a=1\), to mamy odpowiedź, zawierającą przykładowe równanie:
Odpowiedź: \(x^2-4x+2=0\).
Wzory Viete'a dla wielomianu n-tego stopnia
Wzory Viete'a obowiązują także dla wielomianów wyższego stopnia niż drugi. Poniżej zamieszczamy odpowiednie relacje między pierwiastkami \(x_1, x_2, ... x_n\) równania \(x^n+a_{n-1}x^{n-1}+...+a_0=0\).
\(x_1+x_2+...+x_n=-a_{n-1}\)
\({x_1x_2+x_1x_3+...+x_{n-1}x_n=a_{n-2}}\)
\({x_1x_2x_3+x_1x_2x_4+...+x_{n-2}x_{n-1}x_n=-a_{n-3}}\)
\({...}\)
\(x_1x_2...x_n=(-1)^na_0\)
Zastosujmy powyższy wzór dla równania kwadratowego, aby dobrze go zrozumieć.
Mamy ogólną postać równania kwadratowego
\(ax^2+bx+c=0\). Aby dostosować go do postaci \(x^n+a_{n-1}x^{n-1}+...+a_0=0\), musimy podzielić obie strony równania przez \(a\).
\(ax^2+bx+c=0/:a\)
\( x^2+\frac{b}{a}+\frac{c}{a}=0\)
Zatem \(a_{n-1}=\frac{b}{a}\) oraz \(a_{n-2}=\frac{c}{a}\). Otrzymaliśmy wzory z początku artykułu:
\(x_1+x_2=-\frac{b}{a}\)
\(x_1\cdot{x_2}=\frac{c}{a}\)
Wzory Viete'a 3-ego stopnia
\(x_1+x_2+x_3=-\frac{b}{a}\)
\(x_1\cdot x_2\cdot x_3=-\frac{d}{a}\)
\(x_1\cdot x_2+x_1\cdot x_3+x_2\cdot x_3=\frac{c}{a}\)
Wzory Viete'a 4-ego stopnia
\(ax^4+bx^3+cx^2+dx+e=0{,\ }a\neq 0\)
\(x_1+x_2+x_3+x_4=\frac{-b}{a}\)
\(x_1x_2+x_1x_3+x_1x_4+x_2x_3+x_2x_4+x_3x_4=\frac{c}{a}\)
\(x_1x_2x_3+x_1x_2x_4+x_1x_3x_4+x_2x_3x_4=\frac{-d}{a}\)
\(x_1x_2x_3x_4=\frac{e}{a}\)
Zadania z rozwiązaniami

Zadanie nr 1.
Kwadrat różnicy pierwiastków równania kwadratowego \(x^2-x+m=0\) jest równy 17. Znaleźć rozwiązanie tego równania.

Zadanie nr 2.
Suma kwadratów pierwiastków równania kwadratowego \(x^2+dx+1=0\) jest równa 7. Znaleźć rozwiązanie tego równania.

Zadanie nr 3.
Znaleźć równanie kwadratowe, którego suma kwadratów pierwiastków jest równa \(\frac{17}{4}\), a suma odwrotności pierwiastków jest równa \(\frac{3}{2}\).

Zadanie nr 4.
Rozwiązać równanie kwadratowe \(x^2+mx-3=0\), jeśli wiadomo, że suma odwrotności pierwiastków równania jest równa 2.

Zadanie nr 5 — maturalne.
Dany jest trójmian kwadratowy \(f(x)=x^2+2(m+1)x+6m+1\). Wyznacz wszystkie rzeczywiste wartości parametru m, dla których ten trójmian ma dwa różne pierwiastki \(x_1\), \(x_2\) tego samego znaku, spełniające warunek \(|x_1-x_2|<3\).

Zadanie nr 6 — maturalne.
Dany jest trójmian kwadratowy \(f(x)=(m+1)x^2+2(m-2)x-m+4\). Wyznacz wszystkie wartości parametru \(m\), dla których trójmian \(f\) ma dwa różne pierwiastki rzeczywiste \(x_1, x_2\), spełniające warunek \(x_1^2-x_2^2=x_1^4-x_2^4\).

Zadanie nr 7 — maturalne.
Wyznacz wszystkie wartości parametru \(m\), dla których równanie \(4x^2−6mx+(2m+ 3)(m− 3)=0\) ma dwa różne rozwiązania rzeczywiste \(x_1\) i \(x_2\), przy czym \(x_1<x_2\), spełniające warunek \((4x_1-4x_2-1)(4x_1-4x_2+1)<0\).

Zadanie nr 8 — maturalne.
Wyznacz wszystkie wartości parametru \(m\), dla których równanie \(x^2 + (m+1)x−m^2+1=0\) ma dwa rozwiązania rzeczywiste \(x_1\) i \(x_2\) \((x_1\neq x_2)\), spełniające warunek \(x^3_1+x^3_2>−7x_1x_2\).

Zadanie nr 9 — maturalne.
Wyznacz wszystkie wartości parametru \(m\), dla których funkcja kwadratowa \(f\) określona wzorem \(f(x)=(2m +1)x^2+(m+2)x+m−3\) ma dwa różne pierwiastki rzeczywiste \(x_1, x_2\), spełniające warunek \((x_1- x_2)^2+5x_1x_2 \geq 1\).

Zadanie nr 10 — maturalne.
Dane jest równanie kwadratowe \(x^2−(3m+2)x+2m^2+7m−15=0\) z niewiadomą \(x\). Wyznacz wszystkie wartości parametru \(m\), dla których różne rozwiązania \(x_1\) i \(x_2\)tego równania istnieją i spełniają warunek \(2x^2_1+5x_1x_2+2x^2_2=2\).

Zadanie nr 11 — maturalne.
Wyznacz wszystkie wartości parametru \(m\), dla których równanie \(x^2-(m+1)x+m=0\) ma dwa różne rozwiązania rzeczywiste \(x_1\) oraz \(x_2\), spełniające warunki: \(x_1\neq 0, x_2\neq 0\) oraz \(\frac{1}{x_1}+\frac{1}{x_2}+2=\frac{1}{x_1^2} +\frac{1}{x_2^2}\).

Zadanie nr 12 — maturalne.
Wyznacz wszystkie wartości parametru \(m\neq 2\), dla których równanie
\(x^2+4x-\frac{m-3}{m-2}=0\)
ma dwa różne rozwiązania rzeczywiste \(x_1, x_2\) spełniające warunek \(x_1^3+x_2^3>-28\). Zapisz obliczenia.

Zadanie nr 13.
Dla jakich wartości parametru \(m\) suma odwrotności pierwiastków równania \(x^2-2(m+1)x+(m^2+3m-18)=0\) ma wartość ujemną?
Powiązane materiały
© medianauka.pl, 2009-07-21, A-272
Data aktualizacji artykułu: 2023-05-06

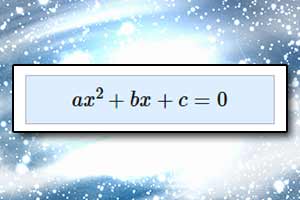 Równanie kwadratowe
Równanie kwadratowe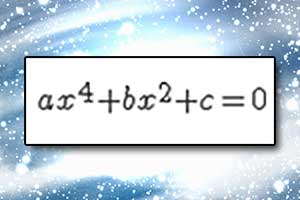 Równanie dwukwadratowe
Równanie dwukwadratowe Równanie kwadratowe z parametrem
Równanie kwadratowe z parametrem Równanie kwadratowe — podstawy
Równanie kwadratowe — podstawy