Równanie dwukwadratowe

Równanie w postaci nazywamy równaniem dwukwadratowym

Aby rozwiązać równanie dwukwadratowe wystarczy dokonać podstawienia z=x², wówczas równanie dwukwadratowe sprowadza się do zwykłego równania kwadratowego. Prześledźmy to na przykładzie:

Przykład

Rozwiązać równanie .

Stosujemy podstawienie: z=x². Otrzymujemy zatem równanie:

Obliczamy wyróżnik trójmianu kwadratowego:
$\Delta=b^2-4ac=100-36=64\\z_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{10-8}{2}=1\\z_1=\frac{-b+\sqrt{\Delta}}{2a}=\frac{10+8}{2}=9$

Możemy teraz zapisać, że
$z_1=x^2=1\vee{z_2=x^2=9}$

Stąd
$x=1,\quad{x=-1},\quad{x=3},\quad{x=-3}$

Zadania z rozwiązaniami

Zadania związane z tematem:
Równanie dwukwadratowe

Zadanie - równanie dwukwadratowe
Rozwiązać równanie

Pokaż rozwiązanie zadania

Zadanie - równanie dwukwadratowe
Rozwiązać równanie

Pokaż rozwiązanie zadania

Inne zagadnienia z tej lekcji

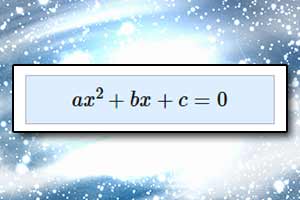Równanie kwadratowe
Równanie w postaci ax^2+bx+c=0 nazywamy równaniem kwadratowym lub równaniem drugiego stopnia.

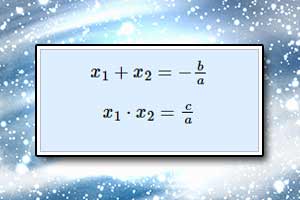Wzory Viete'a
Jeżeli równanie kwadratowe ma pierwiastki, to prawdziwe są wzory Viete'a: x_1+x_2=-\frac{b {a} x_1\cdot{x_2}=\frac{c}{a}.

Równanie kwadratowe z parametrem
Czasem w równaniach stosuje się oznaczenia literowe - parametry. W takim równaniu musimy wskazać niewiadomą. Parametryzujemy równania w celu jego uogólnienia.

Test wiedzy
Sprawdź swoje umiejętności z materiału zawartego w tej lekcji.